
题目列表(包括答案和解析)
 x+1 。
x+1 。 个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒。
个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒。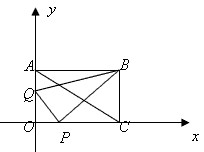
 交于点A(3,6).
交于点A(3,6).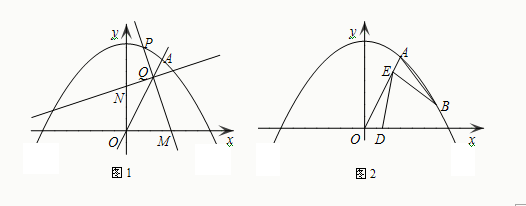
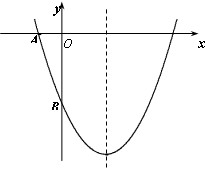
如图,用一根长为18米的篱笆靠墙围成一个长方形的空地用于绿化,且平行墙的一边为长,墙的长为12米。

(1)若长方形的长比宽多1.5米,此时长、宽各是多少米?
(2)在与墙平行的一边开设一个宽为1米的门(用其它材料),使长方形的长比宽多4米,此时它所围成的长方形的面积是多少米2?
(3)若每块长方形草皮长1米、宽0.5米,每块草皮30元,铺满整块绿化地所购买的草皮不超过2400元,请试探究符合条件的长方形的长和宽的长度(长>宽且长、宽取整数)?
【解析】(1)设长方形的宽为x米,则长为(x+1.5)米,列方程求解
(2)设长方形的宽为y米,列方程求出长,从而求得长方形的面积
(3)设长方形的宽为m米,则长为(18-2m)米,列不等式组求整数解,进行讨论
如图,用一根长为18米的篱笆靠墙围成一个长方形的空地用于绿化,且平行墙的一边为长,墙的长为12米。

(1)若长方形的长比宽多1.5米,此时长、宽各是多少米?
(2)在与墙平行的一边开设一个宽为1米的门(用其它材料),使长方形的长比宽多4米,此时它所围成的长方形的面积是多少米2?
(3)若每块长方形草皮长1米、宽0.5米,每块草皮30元,铺满整块绿化地所购买的草皮不超过2400元,请试探究符合条件的长方形的长和宽的长度(长>宽且长、宽取整数)?
【解析】(1)设长方形的宽为x米,则长为(x+1.5)米,列方程求解
(2)设长方形的宽为y米,列方程求出长,从而求得长方形的面积
(3)设长方形的宽为m米,则长为(18-2m)米,列不等式组求整数解,进行讨论
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com