
题目列表(包括答案和解析)
如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴与x轴的正半轴于E、F两点.


(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)连接EF,设△BEF与△BFC的面积之差为S,问:当CF为何值时S最小,并求出这个最小值.
如图,在直角坐标系中,直线![]() 分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=30°,AB=4,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为 ▲ .
分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=30°,AB=4,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为 ▲ .

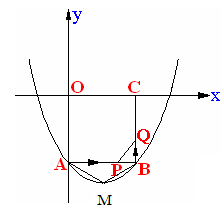
如图,在平面直角坐标系xOy中, 正方形OABC的边长为2cm, 点A、C分别在y轴的负半轴和x轴的正半轴上, 抛物线y=a![]() +bx+c经过点A、B,最低点为M,且
+bx+c经过点A、B,最低点为M,且![]() =
=![]()
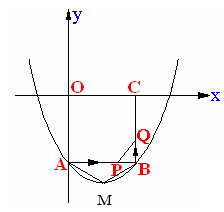
(1)求此抛物线的解析式.,并说明这条抛物线是由抛物线y=a![]() 怎样平移得到的。
怎样平移得到的。
(2)如果点P由点A开始沿着射线AB以2cm/s的速度移动, 同时点Q由点B开始沿BC边以1cm/s的速度向点C移动,当其中一点到达终点时运动结束.
①在运动过程中,P、Q两点间的距离是否存在最小值,如果存在,请求出它的最小值。
②当PQ取得最小值时, 在抛物线上是否存在点R, 使得以P、B、Q、R为顶点的四边形是梯形? 如果存在, 求出R点的坐标, 如果不存在, 请说明理由.
 ABC中,
ABC中, ABC=
ABC= BAC=
BAC=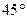 ,点P在AB上,AD
,点P在AB上,AD CP,BE
CP,BE CP,垂足分别为D、E,已知DC=2,求BE的长。
CP,垂足分别为D、E,已知DC=2,求BE的长。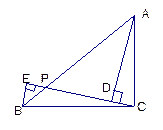
 +bx+c经过点A、B,最低点为M,且
+bx+c经过点A、B,最低点为M,且 =
=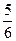
 怎样平移得到的。
怎样平移得到的。 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com