如图，平面直角坐标系中，点A坐标（2,0），点B是y轴上的一个动点，连结AB，取AB中点M，将线段AM绕着点A顺时针方向旋转90°得到线段AN，连结ON、BN，ON与AB所在直线交于点P，设点B的坐标为（0，t）

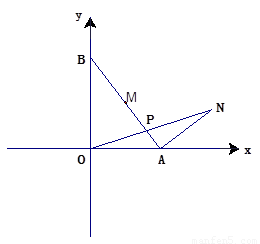
1.（1）当t>0时，用t的代数式表示点N的坐标；

2.（2）设△OBN的面积为S，求S关于t的函数关系式；

3.（3）是否存在点B，使得△ABN与△ANP相似？若存在，求出符合条件的点B的坐标，若不存在，请说明理由。

病人按规定的剂量服用某种药物．测得服药后2小时，每毫升血液中的含药量达到最大值为4毫克．已知服药后，2小时前每毫升血液中的含药量y（毫克）与时间x（小时）成正比例；2小时后y与x成反比例（如图所示）．根据以上信息解答下列问题：

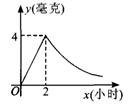
1.求当0≤x≤2时，y与x的函数关系式

2.求当x>2时，y与x的函数关系式

3.若每毫升血液中的含药量不低于2毫克时治疗有效，则服药一次，治疗疾病的有效时间是多长？

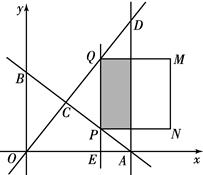
如图，直线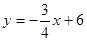分别与x轴、y轴交于A、B两点；直线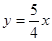与AB交于点C，与过点A且平行于y轴的直线交于点D.点E从点A出发，以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线，分别交直线AB、OD于P、Q两点，以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分（阴影部分）的面积为S（平方单位），点E的运动时间为t（秒）.
（1）求点C的坐标.
（2）当0<t<5时，求S与t之间的函数关系式.
（3）求（2）中S的最大值.
（4）当t>0时，直接写出点（4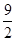，）在正方形PQMN内部时t的取值范围.
【参考公式：二次函数y=ax²+bx+c图象的顶点坐标为（）.】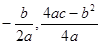

函数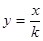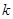（为常数）的图像经过点（–1，–2），当x>0时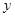，随着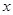的增大而        ．（填增大或减小）

    已知一次函数(b为常数)的图象与反比例函数（k为常数．且）

的图象相交于点P(3．1)．

    (I) 求这两个函数的解析式；

(II) 当x>3时，试判断与的大小．井说明理由。