练习册

  • 练习册
  • 试题
    2．一个小球由静止开始在一个斜坡上向下滚动.其速度每秒增加2米.到达坡底时.小球速度达到40米/秒． 与时间t(秒)之间的函数关系式, (2)求3.5秒时小球的速度, (3)求几秒时小球的速度为16米/秒． 【查看更多】

     

    题目列表(包括答案和解析)

    (科内交叉题)一个角的补角与这个角的余角的和比平角少10°，求这个角．

    查看答案和解析>>

    (科外交叉题)如图所示，当光线从空气射入水中时，光线的传播方向发生了改变，这就是光的折射现象．若∠1＝42°，∠2＝28°，则光的传播方向改变了________度．

    查看答案和解析>>

    从一个等边三角形（如图①）开始，把它的各边分成相等的三段，再在各边中间一段上向外画出一个小等边三角形，形成六角星图形（如图②）；然后在六角星各边上，用同样的方法向外画出更小的等边三角形，形成一个有18个尖角的图形（如图③）；如果在其各边上，再用同样的方法向外画出更小的等边三角形（如图④）．如此继续下去，图形的轮廓就能形成分支越来越多的曲线，这就是瑞典数学家科赫将雪花理想化得到的科赫雪花曲线．
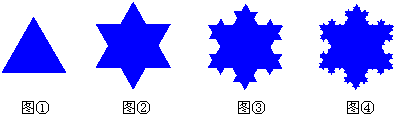
    精英家教网
    如果设原等边三角形边长为a，不妨把每一次的作图变化过程叫做“生长”，例如，第1次生长后，得图②，每个小等边三角形的边长为
    1
    3
    a    ，所形成的图形的周长为4a．
    请填写下表：（用含a的代数式表示）
    第1次
    生长后    		 第2次
    生长后    		 第3次
    生长后    		 … 第n次
    生长后
    每个小等边
    三角形的边长
    1
    3
    a
     
     
    		 …
     
    所形成的
    图形的周长    		 4a
     
     
    		 …
     

    查看答案和解析>>

    从一个等边三角形（如图①）开始，把它的各边分成相等的三段，再在各边中间一段上向外画出一个小等边三角形，形成六角星图形（如图②）；然后在六角星各边上，用同样的方法向外画出更小的等边三角形，形成一个有18个尖角的图形（如图③）；如果在其各边上，再用同样的方法向外画出更小的等边三角形（如图④）．如此继续下去，图形的轮廓就能形成分支越来越多的曲线，这就是瑞典数学家科赫将雪花理想化得到的科赫雪花曲线．

    如果设原等边三角形边长为a，不妨把每一次的作图变化过程叫做“生长”，例如，第1次生长后，得图②，每个小等边三角形的边长为数学公式，所形成的图形的周长为4a．
    请填写下表：（用含a的代数式表示）
    第1次
    生长后    		第2次
    生长后    		第3次
    生长后    		…第n次
    生长后
    每个小等边
    三角形的边长    		数学公式________________…________
    所形成的
    图形的周长    		4a________________…________

    查看答案和解析>>

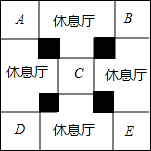    世博会某国国家馆模型的平面图如图所示，其外框是一个大正方形，中间四个大小相同的小正方形（阴影部分）是支撑展馆的核心筒，标记了字母的五个大小相同的正方形是展厅，剩余的四个大小相同的休息厅，已知核心筒的正方形边长比展厅的正方形边长的一半多1米．
    （1）若设展厅的正方形边长为x米，用含x的代数式表示核心筒的正方形边长为
    （
    1
    2
    x+1）
    （
    1
    2
    x+1）
    米．
    （2）若设核心筒的正方形边长为y米，求该模型的平面图外框大正方形的周长．（用含y的代数式表示）
    （3）若设核心筒的正方形边长为y米，用含y的代数式表示每个休息厅的图形周长为
    （14y-8）
    （14y-8）
    米．

    查看答案和解析>>


    同步练习册答案