简单的轴对称图形
（1）角是轴对称图形，它的对称轴是它的平分线所在的直线．角平分线上的点到______的距离相等；到一个角的两边距离相等的点，在______上．
（2）线段是轴对称图形，线段的______是它的一条对称轴．线段的______上的点到这条线段两个端点的距离相等．______的点，在这条线段的垂直平分线上．
轴对称和轴对称图形的区别与联系：
区别：（1）轴对称是说两个图形的位置关系，轴对称图形是说一个具有特殊形状的图形；
（2）轴对称是对两个图形说的，轴对称图形是对一个图形说的．
联系：（1）它们的定义中，都有沿某直线折叠，图形重合；
（2）如果把两个成轴对称的图形看成一个整体，那么它就是一个轴对称图形，反过来，把轴对称图形的两部分当作两个图形，那么这两个图形成轴对称．
提问：等腰三角形的判定与性质？

利用轴对称，我们还可以用简单的轴对称图形组成新的图形．发挥你的想像力，以两个圆、两个三角形、两条平行线为条件，画出一个独特且有意义的图形，并写上一两句贴切诙谐的解说词．例如：

在学习“轴对称现象”内容时，王老师让同学们寻找身边的轴对称图形，小明有一副三角尺和一个量角器（如图所示）．

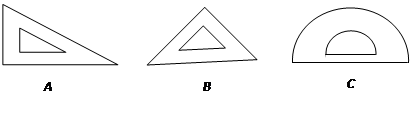
⑴小明的这三件文具中，可以看做是轴对称图形的是___________（填字母代号）；

⑵小红也有同样的一副三角尺和一个量角器．若他们分别从自己这三件文具中随机取出一件，则可以拼成一个轴对称图案的概率是多少？

【解析】（1）考查了轴对称图形的概念；

（2）此题需要两步完成，所以采用列表法比较简单，解题时要注意是放回实验还是不放回实验，此题属于放回实验