练习册

  • 练习册
  • 试题
    1．初步理解一次函数及其图象的性质,初步体会方程与函数的关系． 【查看更多】

     

    题目列表(包括答案和解析)

    一次函数的图象

    (1)一次函数的图象是一条________．

    (2)当k＞0时，直线从左到右向________，即y随x的增大而________．

    (3)当k＜0时，直线从左到右向________，即y随x的增大而________．

    理解一次函数的图象和性质时，一定要与正比例函数对照起来．如在增减性这一条性质上它们是一致的；在位置这一条性质上，一次函数是由正比例函数上、下平移|b|个单位而构成．

    画一次函数图象时，一般是找图象与横轴与纵轴的交点，即________和________如y＝2x＋1的图象是过(0，1)和(－，0)的一条直线．

    查看答案和解析>>

    （2012•佛山）规律是数学研究的重要内容之一．
    初中数学中研究的规律主要有一些特定的规则、符号（数）及其运算规律、图形的数值特征和位置关系特征等方面．
    请你解决以下与数的表示和运算相关的问题：
    （1）写出奇数a用整数n表示的式子；
    （2）写出有理数b用整数m和整数n表示的式子；
    （3）函数的研究中，应关注y随x变化而变化的数值规律（课本里研究函数图象的特征实际上也是为了说明函数的数值规律）．
    下面对函数y=x2的某种数值变化规律进行初步研究：
    xi 0 1 2 3 4 5 …
    yi 0 1 4 9 16 25 …
    yi+1-yi 1 3 5 7 9 11 …
    由表看出，当x的取值从0开始每增加1个单位时，y的值依次增加1，3，5…
    请回答：
    ①当x的取值从0开始每增加
    1
    2
    个单位时，y的值变化规律是什么？
    ②当x的取值从0开始每增加
    1
    n
    个单位时，y的值变化规律是什么？

    查看答案和解析>>

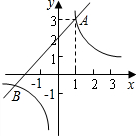    如图，已知一次函数y1=x+m（m为常数）的图象与反比例函数 y2=
    k
    x
    （k为常数，k≠0）的图象相交于点 A（1，3）．
    （1）求这两个函数的解析式及其图象的另一交点B的坐标；
    （2）点C（a，b）在反比例函数 y2=
    k
    x
    的图象上，求当1≤a≤3时，b的取值范围；
    （3）观察图象，写出使函数值y1≥y2的自变量x的取值范围．

    查看答案和解析>>

    （2013•鄂州）下列命题正确的个数是（　　）
    ①若代数式
    		2-2x
    x2-x
    有意义，则x的取值范围为x≤1且x≠0．
    ②我市生态旅游初步形成规模，2012年全年生态旅游收入为302 600 000元，保留三个有效数字用科学记数法表示为3.03×108元．
    ③若反比例函数y=
    m
    x
    （m为常数），当x＞0时，y随x增大而增大，则一次函数y=-2x+m的图象一定不经过第一象限．
    ④若函数的图象关于y轴对称，则函数称为偶函数，下列三个函数：y=3，y=2x+1，y=x2中偶函数的个数为2个．

    查看答案和解析>>

    如图（1）所示，△ABC是直角三角形，BD是斜边上的高，若AB=3，BC=4，AC=5，求BD的长．
    解：因为S△ABC=
    1
    2
    AB•BC，S△ABC=
    1
    2
    AC•BD，所以
    1
    2
    AB•BC=
    1
    2
    AC•BD，
    所以3×4=5BD，则BD=
    12
    5
    ，
    以上求解的基本思想是以三角形的面积不变为相等关系，通过从不同角度表示同一三角形的面积来发现三角形各边及其上的高的关系，这种解决问题的方法我们常称为“面积法”，根据你的理解回答下面的问题：
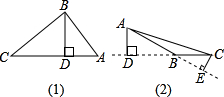    如图（2）所示，△ABC中，AD，CE都是△ABC的高，且AD=3cm，CE=2cm，AB=6精英家教网cm，求CB的长．

    查看答案和解析>>


    同步练习册答案