
题目列表(包括答案和解析)
阅读理解题:
有些与分式计算有关的问题,直接求解有困难,但如果将分式的分子、分母颠倒位置往往能化繁为简,先看下面例题。
例:已知![]() ,求分式
,求分式![]() 的值。
的值。
分析:由于求值的分式中分子是单项式,分母是多项式,且![]() ,于是转化为求
,于是转化为求![]() 的值,因为这与题设
的值,因为这与题设![]() 比较接近。
比较接近。
| a |
| a+1 |
| b |
| b+1 |
| a |
| a+1 |
| ab |
| (a+1)b |
| 1 |
| ab+b |
| 1 |
| b+1 |
| 1 |
| b+1 |
| b |
| b+1 |
| a |
| ab+a+1 |
| b |
| bc+b+1 |
| c |
| ca+c+1 |
| a |
| a+1 |
| b |
| b+1 |
| a |
| a+1 |
| ab |
| (a+1)b |
| 1 |
| ab+b |
| 1 |
| b+1 |
| 1 |
| b+1 |
| b |
| b+1 |
| a |
| ab+a+1 |
| b |
| bc+b+1 |
| c |
| ca+c+1 |
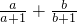 的值.
的值. 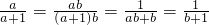
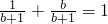
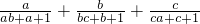 的值.
的值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com