
题目列表(包括答案和解析)
阅读(1)的推导并填空,然后解答第(2)题。
当,![]()
又![]() ,
,
![]() ,
,![]()
即:无论x怎样变化,![]() 的所有取值中,以A为最大;且在
的所有取值中,以A为最大;且在![]() 时,
时,![]() 的值等于A,其中,用
的值等于A,其中,用![]() 表示,A=_______________,B=_______________;
表示,A=_______________,B=_______________;
(2
)为了绿化城市,我市准备在如图的矩形ABCD内规划一块地面,修建一个矩形草坪PQRC。按计划要求,草坪的两边RC与CP分别在BC和CD上,且草坪不能超过文物保护区△AEF的边界EF。经测量知,AB=CD=100m,BC=AD=80m,AE=30m,AF=20m。应如何确定草坪的位置,才能使草坪占地面积最大又符合设计要求?并求出这个最大面积(结果保留到个位,解答时可应用(1)的结论)。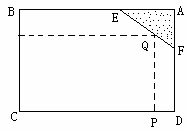

| k2 |
| a2 |
| k |
| a |
| k |
| a |
| k2 |
| a2 |
| k |
| a |
| k |
| k2 |
| a2 |
| 1 |
| 6 |
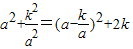 (k为常数且k>0,a≠0),
(k为常数且k>0,a≠0),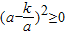
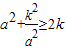
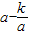 =0,即
=0,即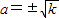 时,
时,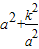 取得最小值2k.
取得最小值2k. ?若存在,请求出m的值;若不存在,请说明理由.
?若存在,请求出m的值;若不存在,请说明理由.

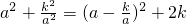 (k为常数且k>0,a≠0),
(k为常数且k>0,a≠0),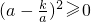
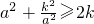
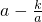 =0,即
=0,即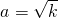 时,
时,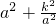 取得最小值2k.
取得最小值2k. ?若存在,请求出m的值;若不存在,请说明理由.
?若存在,请求出m的值;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com