
题目列表(包括答案和解析)

 27、阅读:我们把边长为1的等边三角形PQR沿着边长为整数的正n(n>3)边形的边按照如图1的方式连续转动,当顶点P回到正n边形的内部时,我们把这种状态称为它的“点回归”;当△PQR回到原来的位置时,我们把这种状态称为它的“三角形回归”.
27、阅读:我们把边长为1的等边三角形PQR沿着边长为整数的正n(n>3)边形的边按照如图1的方式连续转动,当顶点P回到正n边形的内部时,我们把这种状态称为它的“点回归”;当△PQR回到原来的位置时,我们把这种状态称为它的“三角形回归”.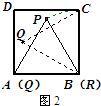


 4、如图是某厂连续7年产量增长率(相对于上年的增长率)统计图,仔细观察图形,下列说法正确的是( )
4、如图是某厂连续7年产量增长率(相对于上年的增长率)统计图,仔细观察图形,下列说法正确的是( )如图是一个装饰物连续旋转闪烁所成的三个图形,照此规律下一个呈现的图形是( )

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com