
题目列表(包括答案和解析)
阅读下面的文章,完成文后问题:
光年和纳米在阅读报刊、杂志或科技书刊时,有时我们会看到“光年”“纳米”这两个名称,你知道它们的含义吗?
光年是天文学中使用的距离单位,简记为l.y.,主要用于度量太阳系外天体的距离.1光年是指光在真空中经历一年所走的距离.真空中光速为c=299792.458km/s,而1年≈60×60×24×365.25(秒),故1光年≈299792.458×60×60×24×365.25≈9.46× km.
km.
即约等于9.46万亿km.
离太阳最近的恒星(半人马座比邻星)与太阳的距离约为4.22光年.银河系的直径约为10万光年.人类所观测的宇宙速度已达到150亿光年,同学们,你能算出这些距离等于多少km吗?从中你是否可以体会到用光年作单位的优越性?
光年是表示较大距离的一个单位,而纳米则是表示微小距离的单位,简记为nm.1nm= m,即1m=
m,即1m=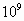 nm.我们通常使用的尺上的一小格是1mm,1mm=
nm.我们通常使用的尺上的一小格是1mm,1mm= m,可是,1mm=
m,可是,1mm= nm,易知1nm相当于1mm的一百万分之一.可想而知,1nm是多么的小.
nm,易知1nm相当于1mm的一百万分之一.可想而知,1nm是多么的小.
当粒子的大小处在1nm~100nm范围内,可称为纳米粒子,纳米粒子的尺寸小,表面积大,具有高度的活性.因此,利用纳米粒子可制备活性极高的催化剂,在火箭固体燃烧中掺入铝的纳米微粒,可提高燃烧效率.利用铁磁纳米材料可制成磁性信用卡、磁性钥匙以及高性能录像带等.利用纳米材料等离子共振频率的可调性可制成隐形飞机的涂料.纳米材料的表面积大,对外界环境(物理的或化学的)十分敏感,在制造传感器方面是很有前途的材料,目前也开发出测量温度、热辐射和检测各种特定气体的传感器,纳米材料在生物和医学中也有重要应用.
纳米材料科学是20世纪80年代末诞生并正在崛起的科技新领域,它将成为跨世纪的科技热点之一.
用科学记数法表示:4.22光年=________km;10万光年=________km;4036m=________nm.
情境一
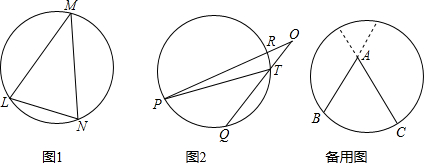
我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角.我们还知道:①圆心角的度数等于与它所对的弧的度数,②同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.由此,小明得到一个正确的结论:圆周角的度数等于它所对的弧的度数的一半.如图1,∠LMN=![]()
![]() .
.
问题1 填空:如图1,如果![]() 的度数是80,那么∠LMN的度数是______.
的度数是80,那么∠LMN的度数是______.
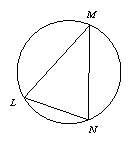 图
图
1
情境二
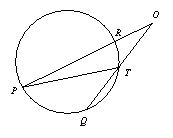
小明把顶点在圆外,并且两边都和圆相交的角叫圆外角,并继续探索.
如图2,∵∠PTQ是△OPT的一个外角,
∴∠PTQ=∠O+∠P.
∴∠O=∠PTQ -∠P.
∵圆周角的度数等于它所对的弧的度数的一半(已在情境一中
证明),
∴∠PTQ=![]()
![]() ,∠P=
,∠P=![]()
![]() .
.
∴∠O=∠PTQ -∠P=![]()
![]() -
-![]()
![]() =
=![]() (
(![]() -
-![]() ).
).
经历了上述探索、证明过程,小明发现了“圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半”这个正确结论.
问题2 填空:如图2,如果![]() =80°,
=80°,![]() =20°,那么∠O=______°.
=20°,那么∠O=______°.
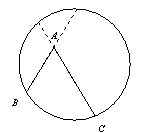
问题3 类比情境二的内容,请你就角的顶点在圆内的情况进行探索.写出你的发现,并证明你的结论.
| 1 |
| 2 |
 |
| LN |
 |
| LN |
| 1 |
| 2 |
 |
| PQ |
| 1 |
| 2 |
 |
| RT |
| 1 |
| 2 |
 |
| PQ |
| 1 |
| 2 |
 |
| RT |
| 1 |
| 2 |
 |
| PQ |
 |
| RT |
 |
| PQ |
 |
| RT |

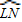 .
. 的度数是80,那么∠LMN的度数是______.
的度数是80,那么∠LMN的度数是______.
 ,∠P=
,∠P=
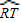 .
.
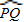 -
-
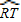 =
= (
(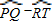 ).
).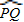 =80°,
=80°,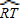 =20°,那么∠O=______°.
=20°,那么∠O=______°.

 .
.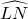 的度数是80,那么∠LMN的度数是________.
的度数是80,那么∠LMN的度数是________.
 ,∠P=
,∠P=
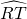 .
.
 -
-
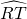 =
= (
(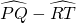 ).
). =80°,
=80°,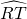 =20°,那么∠O=________°.
=20°,那么∠O=________°.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com