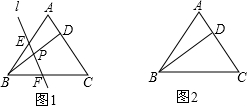
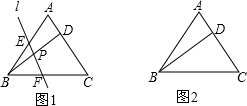
在等边△ABC中,点D为AC上一点,连接BD,直线l与线段BA、BD、BC分别相交于点E、P、F,且∠BPF=60°.
(1)如图1,写出图中所有与△BDC相似的三角形,并选择其中一对给予证明;
(2)若直线l向右平移,与线段BA、BD、BC或其延长线分别相交于E、P、F,请在图2中画出一个与图1位置不尽相同的图形(其它条件不变),此时,(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
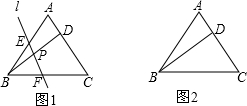
(3)探究:如图1,当BD满足什么条件时(其它条件不变),△BPE的面积是△BPF的面积的2倍?请写出探究结果,并说明理由.(说明:结论中不得含有未标识的字母).