
题目列表(包括答案和解析)
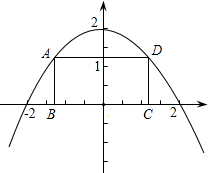 如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.
如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.| b |
| 2a |
| 4ac-b2 |
| 4a |
 (1997•昆明)甲、乙两人分别从相距18公里的A、B两地同时相向而行,甲以4公里/小时的平均速度步行,乙以每小时比甲快1公里的平均速度步行,相遇而止.
(1997•昆明)甲、乙两人分别从相距18公里的A、B两地同时相向而行,甲以4公里/小时的平均速度步行,乙以每小时比甲快1公里的平均速度步行,相遇而止.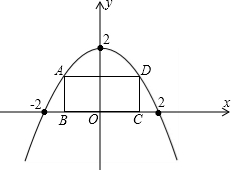 x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.
x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com