
题目列表(包括答案和解析)
 ,即AD=bcosA,所以BD=c-AD=c-bcosA.
,即AD=bcosA,所以BD=c-AD=c-bcosA.
在平面内,旋转变换是指某一图形绕一个定点按顺时针或逆时针旋转一定的角度得到新位置图形的一种变换.
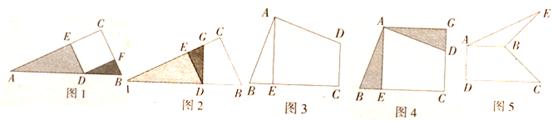
活动一:如图l,在Rt△ABC中,D为斜边AB上的一点,AD =2,BD =1,且四边形DECF是正方形,在求阴影部分面积时,小明运用图形旋转的方法,将△DBF绕点D逆时针旋转90°,得到△DGE(如图2所示),小明一眼就看出答案,请你写出阴影部分的面积:________.
活动二:如图3,在四边形ABCD中,AB=AD,∠BAD=∠C=90°,BC =5,CD =3,过点A作AE⊥BC,垂足为点E,小明仍运用图形旋转的方法,将△ABE绕点A逆时针旋转90°,得到△ADC(如图4所示),则:
(1)四边形AECG是怎样的特殊四边形?答:___________;
(2)AE的长是______________.
活动三:如图5,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC绕点B逆时针旋转90°得到线段BE,连结AE.若AB =2,DC =4,求△ABE的面积.
在平面内,旋转变换是指某一图形绕一个定点按顺时针或逆时针旋转一定的角度得到新位置图形的一种变换.
活动一:如图l,在Rt△ABC中,D为斜边AB上的一点,AD =2,BD =1,且四边形DECF是正方形,在求阴影部分面积时,小明运用图形旋转的方法,将△DBF绕点D逆时针旋转90°,得到△DGE(如图2所示),小明一眼就看出答案,请你写出阴影部分的面积:________.
活动二:如图3,在四边形ABCD中,AB=AD,∠BAD=∠C=90°,BC =5,CD =3,过点A作AE⊥BC,垂足为点E,小明仍运用图形旋转的方法,将△ABE绕点A逆时针旋转90°,得到△ADC(如图4所示),则:
(1)四边形AECG是怎样的特殊四边形?答:___________;
(2)AE的长是______________.
活动三:如图5,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC绕点B逆时针 旋转90°得到线段BE,连结AE.若AB =2,DC =4,求△ABE的面积.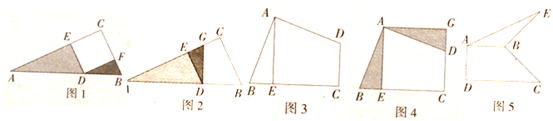
在平面内,旋转变换是指某一图形绕一个定点按顺时针或逆时针旋转一定的角度得到新位置图形的一种变换.
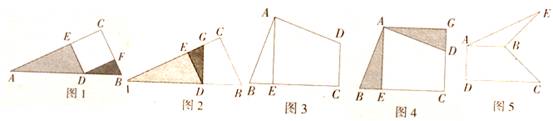
活动一:如图l,在Rt△ABC中,D为斜边AB上的一点,AD =2,BD =1,且四边形DECF是正方形,在求阴影部分面积时,小明运用图形旋转的方法,将△DBF绕点D逆时针旋转90°,得到△DGE(如图2所示),小明一眼就看出答案,请你写出阴影部分的面积:________.
活动二:如图3,在四边形ABCD中,AB=AD,∠BAD=∠C=90°,BC =5,CD =3,过点A作AE⊥BC,垂足为点E,小明仍运用图形旋转的方法,将△ABE绕点A逆时针旋转90°,得到△ADC(如图4所示),则:
(1)四边形AECG是怎样的特殊四边形?答:___________;
(2)AE的长是______________.
活动三:如图5,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC绕点B逆时针 旋转90°得到线段BE,连结AE.若AB =2,DC =4,求△ABE的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com