探索勾股定理时，我们发现“用不同的方式表示同一图形的面积”可以解决线段和（或差）的有关问题，这种方法称为面积法。请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC,BD为腰AC上的高。

(1)若BD=h，M时直线BC上的任意一点，M到AB、AC的距离分别为。

①　　 若M在线段BC上，请你结合图形①证明：= h；　　　　　　　　　　

②　　 当点M在BC的延长线上时，，h之间的关系为　　　　　 （请直接写出结论，不必证明）　　　　　　　　　　　　　　　　　　　　　　　　　

（2）如图②，在平面直角坐标系中有两条直线：y = x + 6 ； ：y = -3x+6 若上的一点M到的距离是3，请你利用以上结论求解点M的坐标。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 图②

[问题情境] 勾股定理是一条古老的数学定理，它有很多证明方法，我国汉代数学家赵爽根据弦图利用面积法进行证明，著名数学家华罗庚曾提出把“数形关系”带到其他星球作为地球人与其他星球“人”进行第一次“谈话”的语言。
[定理表述] 请你根据图（1）中的直角三角形叙述勾股定理（用文字及符号语言叙述）；
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
 
[尝试证明]　以图（1）中的直角三角形为基础可以构造出以a、b为底，以a＋b为高的直角梯形如图（2）。请你利用图（2）验证勾股定理；
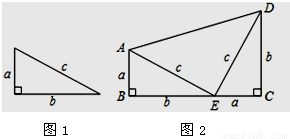
[知识拓展]　利用图(2)的直角梯形，我们可以证明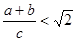，其证明步骤如下：
∵BC＝a＋b，AD＝    　    .
又∵在直角梯形ABCD中有直角腰BC　　　　斜腰AD（填“＞”，“＜”或“＝”），即　　　　　　　。
∴

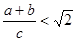
[问题情境] 勾股定理是一条古老的数学定理，它有很多证明方法，我国汉代数学家赵爽根据弦图利用面积法进行证明，著名数学家华罗庚曾提出把“数形关系”带到其他星球作为地球人与其他星球“人”进行第一次“谈话”的语言。

[定理表述] 请你根据图（1）中的直角三角形叙述勾股定理（用文字及符号语言叙述）；

[尝试证明]　以图（1）中的直角三角形为基础可以构造出以a、b为底，以a＋b为高的直角梯形如图（2）。请你利用图（2）验证勾股定理；

[知识拓展]　利用图(2)的直角梯形，我们可以证明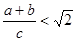，其证明步骤如下：

∵BC＝a＋b，AD＝    　    .

又∵在直角梯形ABCD中有直角腰BC　　　　斜腰AD（填“＞”，“＜”或“＝”），即　　　　　　　。

∴

2006年7月1日青藏铁路正式通车，这条“天路”是中国人建设的世界海拔最高的铁路，它的建成是我国建筑史上的一大杰作．下面给出的是青藏铁路沿线主要地区气象状况的部分数据，请你仔细阅读，解答如下问题：
青藏铁路沿线主要地区气象状况

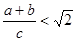
	海拔（m）	大气压（kPa）	最高温度（℃）	最低气温（℃）	平均湿度（%）	大风日（8级）	积雪最深（cm）
西宁	2260	78.0	32.4	-21.9	57
格尔木	2808	72.0	32.8	-29.3	34	16	4
昆仑山口	4767	57.4
五道梁	4495	58.6		-33.2		73.7
风火山	5010	56.1	0	-40.8	17		10
沱沱河	4630	57.41	23.3	-33.8	53	103.0	8
唐古拉山口	5130	53.28
安多	4800	57.33	19.2	-36.7	48
黑河	4507	58.74	22	-41.3	51	52.6	13
拉萨	3658	65.19	29.4	-17.6	42	23.7	4

（1）求青藏铁路沿线（从西宁到拉萨）温度的极差；
（2）绘制青藏铁路沿线：格尔木、五道梁、沱沱河、黑河、拉萨地区全年大风日的频数分布直方图；
（3）计算上述各地区大风日占全年的频率（精确到0.001）填入表格中；

地区	全年大风日频率
格尔木
五道梁
沱沱河
黑河
拉萨

（4）通过阅读本题提供的气象资料，用一两句话谈谈你对青藏铁路建成通车的看法或体会．

　　图案：

　　含义：