如图正方形ABCD和正方形EFGH，F和B重合，EF在AB上，连DH（本题14分）

⑴、由图⑴易知，

①线段AE=CG， AE和CG所在直线互相垂直，且此时易求得②         。

⑵、若把正方形EFGH绕F点逆时针旋转度（图2），⑴中的两个结论是否仍然成立？若成立，选择其中一个加以证明，若不成立，请说明理由。

⑶、若把图⑴中的正方形EFGH沿BD方向以每秒1cm的速度平移，设平移时间为x秒，正方形ABCD和正方形EFGH的边长分别为5cm和1cm，

①在平移过程中，△AFH是否会成为等腰三角形？若能求出x的值，若不能，说明理由．

②在平移过程中，△AFH是否会成为等边三角形？若能求出x的值，若不能，设正方形ABCD和正方形EFGH的边长分别为acm和bcm，则当a、b满足什么关系时，△AFH可以成为等边三角形．

（本题14分）

如图，已知二次函数的图象经过点A（3，3）、B（4，0）和原点O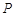．为二次函数图象上的一个动点，过点P作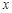轴的垂线，垂足为D（m，0），并与直线OA交于点C．

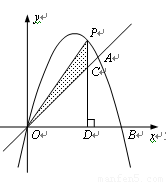
1.⑴ 求出二次函数的解析式；

2.⑵ 当点P在直线OA的上方时，求线段PC的最大值．

3.⑶ 当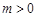时，探索是否存在点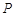，使得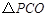为等腰三角形，如果存在，求出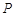的坐标；如果不存在，请说明理由．

(本题14分)阅读：在用尺规作线段等于线段时，小明的具体做法如下：

已知：如图，线段.      

求作：线段,使得线段.

作法: ① 作射线；

② 在射线上截取.

∴线段为所求.

解决下列问题：已知：如图，线段.   

（1）请你仿照小明的作法，在上图中的射线上作线段，使得；（不要求写作法和结论，保留作图痕迹）                

（2）在（1）的条件下，取的中点.若.

①当点在线段上时（画出图形）。段的长.

②当点在线段的延长线上时（画出图形）. 求线段的长.

(本题14分)如图，在平面直角坐标系中．四边形OABC是平行四边形．直线经过O、C两点．点A的坐标为(8，o)，点B的坐标为(11．4)，动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动，同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动，过点P作PM垂直于x轴，与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时，另一点也随之停止运动，设点P、Q运动的时间为t秒()．△MPQ的面积为S．

（1）点C的坐标为___________，直线的解析式为___________．(每空l分，共2分)

（2）试求点Q与点M相遇前S与t的函数关系式，并写出相应的t的取值范围。

（3）试求题(2)中当t为何值时，S的值最大，并求出S的最大值。

（4）随着P、Q两点的运动，当点M在线段CB上运动时，设PM的延长线与直线相交于点N。试探究：当t为何值时，△QMN为等腰三角形？请直接写出t的值．