（三）阅读《植物塑料的兴起》，完成各题。【本题满分15分】
植物塑料的兴起
①据了解，每年我国的包装废弃物约200多万吨，其中有近5％为石油塑料制品垃圾。石油塑料制品的成分主要是聚乙烯或聚苯乙烯，如果直接焚烧这些垃圾，在燃烧过程中会产生对人体致癌的物质。假如填埋，它们历经百年也不会降解，更会污染海洋环境，导致耕地板结，严重破坏生态平衡。最近，一种利用生物技术制造的新型材料——植物塑料的问世，打破了这一局面。
②所谓植物塑料是指由玉米或甘蔗等制造的聚乳酸塑料。现在使用植物塑料的实用化产品已有农业用的地膜和快餐盒等。另外，部分电器产品和服装等也开始使用了植物塑料。植物塑料一直以来被视为与环境亲和的“生物分解塑料”之一。所谓生物分解塑料是指，在自然界中能够通过微生物的作用将其分解为水和二氧化碳的塑料。
③那么，玉米、甘蔗等植物是如何造出塑料的呢?首先，从玉米、甘蔗等植物中萃取出淀粉；接着，用酶将淀粉分解制成麦芽糖或葡萄糖；然后，将麦芽糖或葡萄糖供给微生物食用并发酵，制造出乳酸；最后，将乳酸聚合，造出聚乳酸。这样制作的聚乳酸材料十分坚硬，并具有极高的透明度。但是，聚乳酸单晶在室温下接近玻璃的性质，稍加冲击马上就会碎裂。如果想作为塑料使用，还需要通过掺加柔顺的化合物，另外，由于聚乳酸的熔点只有170℃，作为商品，还必须提高它的耐热性和强度。
④聚乳酸塑料最大特点是在自然界中容易分解。在聚乳酸塑料中加上水，即可变成容易分解的酯。把聚乳酸塑料放入堆肥中，首先通过水分和酶的分解，变成乳酸；再经被称为需氧菌的微生物食之并代谢，最终被分解为水与二氧化碳。而二氧化碳和水原本就是植物从大自然中吸收来的，所以，从整体来说它没给环境增加负担。
⑤用聚乳酸塑料制造的产品具体有什么价值呢？首先，这些塑料来自植物，作为材料来源它优于石油化工塑料。其次，植物能够通过种植获得，所以聚乳酸塑料可说是再生资源或可持续使用的材料。另外，使用谷物为主制造的聚乳酸，不论是焚烧还是在自然界中分解，都不会对环境增加负担。现在世界生产石油化工塑料的年产量是1.5亿吨。如果用聚乳酸制造塑料，这就减少了石油或天然气的消耗。这对化石燃料面临枯竭的现状，无疑是一个最大的福音。
⑥除了日常用品中的广泛适用外，聚乳酸植物塑料在医学方面的应用优势尤为突出，也是目前应用得最为成功的领域。第一是制作医用骨钉。以前治疗骨折等骨科疾病使用的是不锈钢骨钉，病人必经两次手术才能治愈。即第一次手术用钢钉把骨折复位固定，待骨头长好后，再动第二次手术，把钢钉取出。使用聚乳酸植物塑料只需一次手术植入骨钉，病愈的同时，骨钉也降解在人体内。因为降解产生的是二氧化碳和水，所以不会对人体产生不良后果。虽然，目前聚乳酸植物塑料骨钉的价格比不锈钢骨钉高出50％左右，但是多数患者为了避免两次手术的痛苦，还是选择聚乳酸植物塑料骨钉。
⑦另一方面，将聚乳酸植物塑料制成人工脏器的骨架研究也在进行。例如有专家正在聚乳酸植物塑料肝骨架的整个表面上培养肝细胞，制造人造肝脏。用这种方法制造的人造肝脏移到体内，作为骨架部分的聚乳酸植物塑料在体内不久就会被分解吸收，最后留下了与骨架同样形状的肝脏。这是有效利用聚乳酸植物塑料生物分解性质的典范。
⑧要使聚乳酸植物塑料普及，还有一些问题必须解决，特别是制造成本高的问题最令企业头疼。但随着人们环境保护意识的不断提高，聚乳酸塑料必将受到大众的欢迎。为此，聚乳酸植物塑料肯定有发展前景。
（选自《走近科学》2009年第9期）
【小题1】．通读全文，试用简洁的语言概括文章的主要内容。（3分）
                                                                             
                                                                            
【小题2】．文章开篇没有直接从植物塑料写起，而是用较多篇幅先介绍石油塑料制品垃圾的诸多危害，这样写有什么作用？（3分）
                                                                             
                                                                              
【小题3】．第二段和第三段的顺序为什么不能颠倒？（3分）
                                                                             
                                                                                                                  
【小题4】．第⑥自然段主要运用了           、            的说明方法，其目的是
                                                                             
                                                                    （3分）
【小题5】．“目前聚乳酸植物塑料骨钉的价格比不锈钢骨钉高出50％左右”句中加点的词语可以去掉吗？为什么？（3分）
                                                                             
                                                                             

生活常识告诉我们：向一杯糖水(未饱和)溶液中再添加一定量的糖后，虽然糖(溶质)、糖水(溶液)的质量均增加了，但糖水变得更甜了(即溶液的浓度增加了)．又如：班级新转来一名男同学，虽然男同学的人数、班级总人数均增加了，但男生所占的百分比也增加了．生活中诸如此类的例子还很多，将以上问题抽象成数学问题，即可得到如下不等式：＞(其中a，b，m均为正数)．

(1)验证下述不等式(用“＞”、“＝”或“＜”填空)：

①________＝　　　　②________＝

③________＝　　　　④________＝

(2)猜想＜(a，b，m均为正数)成立的条件，并证明你猜想的正确性．

等式中找规律

　　孙海洋是个爱动脑筋的八年级学生，他特别喜欢数学，一有空就看数学课外书，并琢磨书上的问题．有一次，他从一本书中看到了下面一个有趣的问题：

　　仔细观察下面4个等式：

　　3²＝2＋2²＋3

　　4²＝3＋3²＋4

　　5²＝4＋4²＋5

　　6²＝5＋5²＋6

　　……

　　请写出第5个等式，由此能发现什么规律？用公式将发现的规律表示出来．

　　对这个问题，孙海洋感到很新奇，他认真分析题目给出的4个等式，发现有以下一些结构特征：

　　(1)每个等式的左边都是一个自然数的平方，等式的右边都是3个数的和．

　　(2)4个等式的左边依次是3²、4²、5²、6²，它们的底数3、4、5、6是4个连续的自然数，其大小均比所处等式的序号多2．

　　(3)每个等式右边的3个加数也有明显的规律．

　　第1个加数和第3个加数是两个连续的自然数，并且第3个加数等于该等式左边平方数的底数，第2个加数也是一个平方数，底数等于第1个加数．

　　根据以上规律，孙海洋猜想第5个等式应该是7²＝6＋6²＋7．

　　孙海洋进一步归纳了这5个等式的规律，用公式表示为(n＋1)²＝n＋n²＋(n＋1)…①其中n＝2，3，…

　　如果将①式右边变形、左边不变，那么可得(n＋1)²＝n²＋2n＋1…②

　　等式②多么眼熟啊！它不就是完全平方公式的一个具体应用吗？由此可见，孙海洋同学归纳的规律是正确的．

想一想，当n＝0，1时，等式①是否成立？当n为负整数时，等式①是否成立？

关于三角函数有如下的公式：

　　sin（α+β）=sinαcosβ+cosαsinβ①

cos（α+β）=cosαcosβ-sinαsinβ②

tan（α+β）=   (1－tanα·tanβ≠0)……③

利用这些公式可将一些不是特殊角的三角函数转化为特殊角的三角函数来求值，如：

tan105°=tan（45°+60°）==

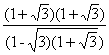　　===－(2＋)。

根据上面的知识，你可以选择适当的公式解决下面实问题：

A

　　如图，Rt△ABC中，∠C＝90°，∠B＝75°，AB＝2，则BC＝（　　）

　　A、　　　B、

C

B

　　C、　　　D、