
题目列表(包括答案和解析)
设抛物线y=ax2+bx-2与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
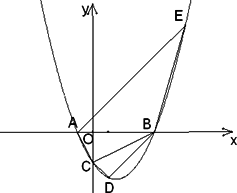
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n)在抛物线上,过点A的直线y=x+1交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
(3)在(2)的条件下,△BDP的外接圆半径等于________.
设抛物线y=ax2+bx-2与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
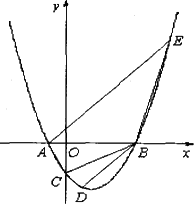
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n)在抛物线上,过点A的直线y=x+1交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
(3)在(2)的条件下,△BDP的外接圆半径等于________.
已知抛物线y=ax2+bx+c的图象交x轴于点A(x0,0)和点B(2,0),与y轴的正半轴交于点C,其对称轴是直线x=-1,tan∠BAC=2,点A关于y轴的对称点为点D.
(1)确定A.C.D三点的坐标;
(2)求过B.C.D三点的抛物线的解析式;
(3)若过点(0,3)且平行于x轴的直线与(2)小题中所求抛物线交于M.N两点,以MN为一边,抛物线上任意一点P(x,y)为顶点作平行四边形,若平行四边形的面积为S,写出S关于P点纵坐标y的函数解析式.
(4)当![]() <x<4时,(3)小题中平行四边形的面积是否有最大值,若有,请求出,若无,请说明理由.
<x<4时,(3)小题中平行四边形的面积是否有最大值,若有,请求出,若无,请说明理由.
(12分)已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
1.(1)求A、B、C三点的坐标;
2.(2)求此抛物线的表达式;
3.(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
4.(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.

已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB.OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
1.求A、B、C三点的坐标;
2.求此抛物线的表达式
3.连接AC、BC,若点E是线段AB上的一个动点(与点A.点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
4.在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com