(1)若敌我相距14千米，且敌军于1小时前以4千米/时的速度逃跑，现在我军以7千米/时的速度追击，问几小时可以追上敌军？

　　(2)甲、乙、丙三人在400米的环形跑道上，同时同地分别以每秒6米、4米、8米的速度跑步出发，且甲、乙反向，甲、丙同向，当丙遇到乙时，即反向迎甲跑，遇上甲时，又反向迎乙跑，如此练习下去，直至甲、乙、丙三人相遇为止，求丙跑了多少米？

　　(3)在学校组织的“献爱心”活动中，七年级一班的学生捐了380元，二班的学生的捐款数是其他两班的平均数，三班学生的捐款数是这三个班总数的，则二班、三班各捐了多少元？

　　(4)夏季是用电高峰，由于电力供应不足和线路超负荷等问题，经常停电．小明家准备一粗一细两根蜡烛，长度相同，粗蜡烛全部点完需要2小时，细蜡烛全部点完需要1小时．今天晚上又停电了，小明同时点上一粗一细两根新蜡烛继续学习，不久就来电了．小明熄灭蜡烛，这时，粗蜡烛的长是细蜡烛长的2倍，问停电多少分钟？

若一个关于x的方程x²＋px＋q＝0的两根分别为x₁，x₂，则x²＋px＋q＝(x－x₁)(x－x₂)．即x²＋px＋q＝x²－(x₁＋x₂)x＋x₁x₂，由于左、右两边相等，∴p＝－(x₁＋x₂)，q＝x₁x₂．这说明以x₁，x₂两数为根的一元二次方程的一次项系数等于这两个数和的相反数，常数项等于这两个数的积，请认真阅读上述材料，完成下面问题：

(1)若a＋b＝4，ab＝2，请你写出一以y为元的一元二次方程，使a、b两数为这个一元二次方程的根；

(2)利用你所学的知识判断(1)中的实数a、b是否存在，说明理由．

在一元二次方程口0中，如果≥0，那么它的两个实数根是，．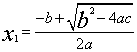

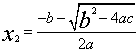通过计算可得，．

由此可见，一元二次方程的两个实数根的和与积是由一元二次方程的系数确定的．

运用上述关系解答下列问题：

(1)设方程的两个实数根分别为、，则+=_________，·=_________.

(2)求方程与方程所有实数根的和．

在一元二次方程ax²+bx+c=0中，如果b²+4ac≥0，那么它的两个根是：

．

通过计算可以得到：x₁+x₂=，x₁x₂=．  

由此可见，一元二次方程的两个根的和、两个根的积都是由一元二次方程的系数确定的．运用上述关系解答下面的问题：

(1)设方程2x²6x1=0的两个根分别为x₁、x₂，则

  x₁+x₂=________，x_l·x₂=________．

(2) 方程x²+3x2=0与方程2x²6x1=0所有实数根的和为多少？

①由一个二元一次方程和一个二元二次方程组成的方程组，一般都可以用___________法来解．

②由一个二元二次方程和一个可以分解的两个二元一次方程的方程组成的方程组，一般是将可分解的二元二次方程通过___________得到两个二元一次方程后再分别与另一个二元二次方程组成___________方程组，再用①的方法解这两个方程组，从而得到原方程组的解．