
题目列表(包括答案和解析)
 如图,四边形ABCD中,E、F、G、H分别为各边的中点,顺次连结E、F、G、H,把四边形EFGH称为中点四边形.连结AC、BD,容易证明:中点四边形EFGH一定是平行四边形.
如图,四边形ABCD中,E、F、G、H分别为各边的中点,顺次连结E、F、G、H,把四边形EFGH称为中点四边形.连结AC、BD,容易证明:中点四边形EFGH一定是平行四边形.| 1 | 4 |
 如图,A.B.C.D四点在同一平面内,并且每三点都不在同一条直线上,读下列语句,按要求画出图形.
如图,A.B.C.D四点在同一平面内,并且每三点都不在同一条直线上,读下列语句,按要求画出图形.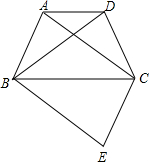 (2013•柳州)如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
(2013•柳州)如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC. 下图是两组对边分别平行的四边形:
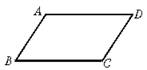
即:AB∥CD,AD∥BC,那么
(1)各对边之间有什么样的数量关系?为什么?
(2)各对角之间有什么样的数量关系?为什么?
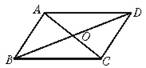
(3)如果连结AC、BD,交点为O,如图,那么AC、BD之间又有什么关系?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com