(本题满分10分)如图，阳春三月里小黄同学在操场上放风筝，风筝从A处起飞，几分钟后便飞到C处，此时，在AQ的延长线上B处的小宋同学发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上．

 1. (1)已知旗杆高10米，若在B处测得旗杆顶点P的仰角为30°，在A处测得点P的仰角为45°，试求A、B之间的距离．

 　2. (2)此时，在A处背向旗杆又测得风筝的仰角为75°，若将绳子在空中视为一条线段，求绳子的长度AC(结果保留根号)．

(本题满分10分)如图，△ABC的三个顶点都在格点上．A(-1,3),  B(-1,-1), C(-3,-3)

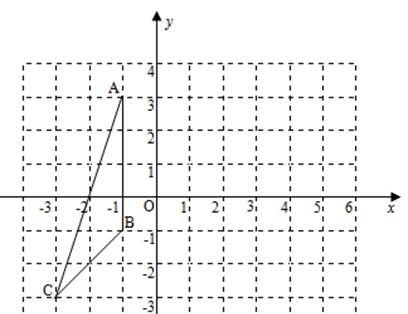
1.（1）画出△ABC绕点A逆时针旋转90°所得图形△AB＇C＇

2.（2）直接写出△AB＇C＇外接圆的圆心D坐标　　 　　．

3.（3）求∠A C＇B＇的正切值．

附加题（共10分）在答题卡上相应题目的答题区域内作答．

友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况．如果你全卷得分低于90分（及格线），则本题的得分将计入全卷总分，但计入后全卷总分最多不超过90分；如果你全卷总分已经达到或超过90分，则本题的得分不计入全卷总分．

1.（5分）计算：          ．

2.（5分）如图，已知直线，，则　　　度．

（本题满分10分）

如图，将OA = 6，AB = 4的矩形OABC放置在平面直角坐标系中，动点M、N以每秒１个单位的速度分别从点A、C同时出发，其中点M沿AO向终点O运动，点N沿CB向终点B运动，当两个动点运动了t秒时，过点N作NP⊥BC，交OB于点P，连接MP．

（1）点B的坐标为　  ；用含t的式子表示点P的坐标为     ；(3分)

（2）记△OMP的面积为S，求S与t的函数关系式（0 < t < 6）；并求t为何值时，S有最大值？(4分)

（3）试探究：当S有最大值时，在y轴上是否存在点T，使直线MT把△ONC分割成三角形和四边形两部分，且三角形的面积是△ONC面积的？若存在，求出点T的坐标；若不存在，请说明理由．(3分)