
题目列表(包括答案和解析)
已知在半径为2的⊙O中,内接三角形ABC的边![]() ,则∠C的度数为( ).
,则∠C的度数为( ).
A.60° B.30° C.60°或120° D.30°或150°
| 3 |
 |
| AC |
 重合,连接AD并延长交BC的延长结于P.
重合,连接AD并延长交BC的延长结于P.在Rt△ABC中,已知两直角边的长分别为5cm、12cm,则该直角三角形外接圆的半径与内切圆的半径分别为( )
A.6cm和2cm B.7.5cm和4cm
C.6.5cm和2cm D.6.5cm和3cm
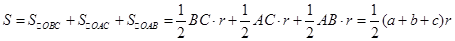 .
.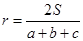 .
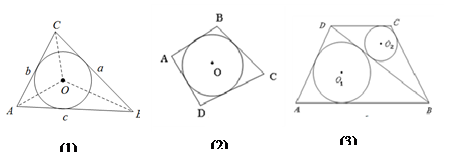
.
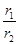 的值.
的值. 方案设计:儿童公园有一块半圆形空地,如图11所示,根据需要欲在此半圆内划出一个三角形区域作为健身场地,其中内接于此三角形的矩形区域为儿童游乐场,已知半圆的直径AB=100米,若使三角形的顶点C在半圆上,且AC=80米.
方案设计:儿童公园有一块半圆形空地,如图11所示,根据需要欲在此半圆内划出一个三角形区域作为健身场地,其中内接于此三角形的矩形区域为儿童游乐场,已知半圆的直径AB=100米,若使三角形的顶点C在半圆上,且AC=80米.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com