
题目列表(包括答案和解析)
阅读下列材料,然后解答后面的问题。
我们知道方程 有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由
有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由 ,得
,得 ,(
,( 、
、 为正整数)
为正整数)  则有
则有 .
.
又 为正整数,则
为正整数,则 为正整数.
为正整数.
由2与3互质,可知: 为3的倍数,从而
为3的倍数,从而 ,代入
,代入 .
. 的正整数解为
的正整数解为
问题:(1)请你写出方程 的一组正整数解:
的一组正整数解:
(2)若 为自然数,则满足条件的
为自然数,则满足条件的 值有 个
值有 个
| A.2 | B.3 | C.4 | D.5 |
 ,(x、y为正整数)
,(x、y为正整数)
 x为正整数,则
x为正整数,则 x为正整数
x为正整数 ×3=2
×3=2  。
。 为自然数,则满足条件的x的值有______个;
为自然数,则满足条件的x的值有______个;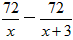 =4;
=4; =4;
=4;阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解。
例.由2x+3y=12得:y=![]() =4-
=4-![]() x,(x、y为正整数)
x,(x、y为正整数)
∴![]() 则有0<x<6
则有0<x<6
又y=4-![]() x为正整数,则
x为正整数,则![]() x为正整数.
x为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入:y=4-![]() ×3=2
×3=2
∴2x+3y=12的正整数解为![]()
问题:(1)请你写出方程2x+y=5的一组正整数解: .
(2)若![]() 为自然数,则满足条件的x的值有 个. ( )
为自然数,则满足条件的x的值有 个. ( )
A.2 B.3 C.4 D.5
(3)九年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案.试确实.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com