
题目列表(包括答案和解析)
| 1 | 2 |
 y轴交于点C.
y轴交于点C.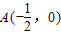 、B(2,0)两点,且与y轴交于点C.
、B(2,0)两点,且与y轴交于点C.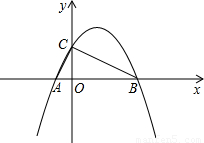


 BC。
BC。  BC。
BC。 (AD+BC)吗?
(AD+BC)吗?学完了《函数的图象》这一节,陈老师在黑板上布置这样一道题:给你一个坐标系,一些半径为1的圆,请将圆合理地在坐标系中摆放,依次连结各圆心,使圆心构成有规则的几何图形,并写出这些图形顶点坐标.
苏阳的作业:
解:摆设图形如图所示

△ABC顶点坐标:A(0,1),B(-1,-1),C(1,-1)
正方形ABCD顶点坐标:A(-1,1),B(-1,-1),C(1,-1),D(1,1)
你能把坐标系旁边的圆“搬”进坐标系中吗(如图)?使圆心连线构成(1)平行四边形,(2)梯形.并写出顶点坐标.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com