3、已知△ABC为锐角三角形，⊙O经过点B，C，且与边AB，AC分别相交于点D，E．若⊙O的半径与△ADE的外接圆的半径相等，则⊙O一定经过△ABC的（　　）

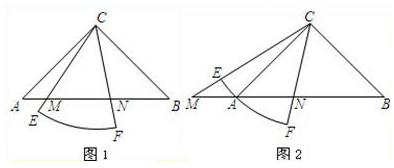
25、已知Rt△ABC中，∠ACB=90°，CA=CB，有一个圆心角为45°，半径的长等于CA的扇形CEF绕点C旋转，且直线CE，CF分别与直线AB交于点M，N．
（Ⅰ）当扇形CEF绕点C在∠ACB的内部旋转时，如图1，求证：MN²=AM²+BN²；
（思路点拨：考虑MN²=AM²+BN²符合勾股定理的形式，需转化为在直角三角形中解决．可将△ACM沿直线CE对折，得△DCM，连DN，只需证DN=BN，∠MDN=90°就可以了．请你完成证明过程．）
（Ⅱ）当扇形CEF绕点C旋转至图2的位置时，关系式MN²=AM²+BN²是否仍然成立？若成立，请证明；若不成立，请说明理由．

已知下列命题：①同旁内角互补；②圆心到直线上一点的距离恰好等于圆的半径，则该直线是圆的切线；③对角线相等且互相垂直的四边形是正方形；④两圆没有公共点则它们的位置关系是外离；⑤已知一圆锥的高为4，母线长为5，则该圆锥的侧面积为15π．其中真命题的个数有（　　）个．