
题目列表(包括答案和解析)
| A、12 | B、13 | C、14 | D、15 |
 ,动点O从A出发以1cm/s的速度沿AC方向向点C匀速运动,同时线段EF从与线段CB重合的位置出发以1cm/s的速度沿BA方向向点C匀速运动.在运动过程中,EF交AC于点G,连接OE、OF.设运动时间为ts(0<t<10),请你解决以下问题:
,动点O从A出发以1cm/s的速度沿AC方向向点C匀速运动,同时线段EF从与线段CB重合的位置出发以1cm/s的速度沿BA方向向点C匀速运动.在运动过程中,EF交AC于点G,连接OE、OF.设运动时间为ts(0<t<10),请你解决以下问题:
 +
+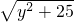 的最小值;
的最小值; +
+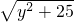 的最小值即为线段______和线段______长度之和的最小值,最小值为______.
的最小值即为线段______和线段______长度之和的最小值,最小值为______.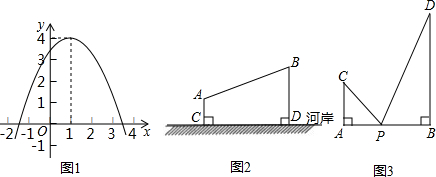
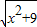 +
+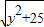 的最小值;
的最小值;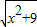 +
+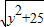 的最小值即为线段______和线段______长度之和的最小值,最小值为______.
的最小值即为线段______和线段______长度之和的最小值,最小值为______.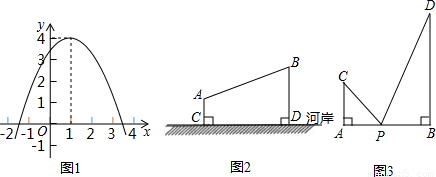
| (23-1)(33-1)(43-1)…(1003-1) |
| (23+1)(33+1)(43+1)…(1003+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com