(本题满分8分)通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对(sad)．如图①在△ABC中，AB＝AC，顶角A的正对记作sad A，这时sad A．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：

（1）sad 60°＝           ．

（2）对于0°＜A＜180°，∠A的正对值sadA的取值范围是

（3）如图②，在Rt△ABC中，∠C＝90°，sin A，试求sad A的值

		B
	B

(本题满分10分)

如图，一艘轮船由A港沿北偏东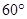方向航行10km至B港，再沿北偏西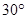方向航行10km到达C港.

    （1）求A、C两港之间的距离（精确到1km）

    （2）求点C相对于点A位置.

(本题满分10分)

如图，一艘轮船由A港沿北偏东方向航行10km至B港，再沿北偏西方向航行10km到达C港.

    （1）求A、C两港之间的距离（精确到1km）

   （2）求点C相对于点A位置.

(本题满分9分)

如图，以为顶点的抛物线与轴交于点．已知、两点坐标分别为(3，0)、(0，4)．

(1)求抛物线的解析式；

(2)设是抛物线上的一点(、为正整数)，且它位于对称轴的右侧．若以、、、为顶点的四边形四条边的长度是四个连续的正整数，求点的坐标；

(3)在(2)的条件下，试问：对于抛物线对称轴上的任意一点，是否总成立?请说明理由．