
题目列表(包括答案和解析)
|
|
|
|
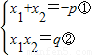 这两个式子揭示了一元二次方程的根与系数之间的关系,且关系式①②中,x1,x2的地位是对等的(即具有对称性,如将x1,x2互换,原关系式不变).类似地,设一元三次方程x3+px2+qx+r=0(p,q,r为常数)的3个根为x1,x2,x3,则x3+px2+qx+r=(x-x1)(x-x2)(x-x3).由此可得方程x3+px2+qx+r=0的根x1,x2,x3与系数p,q,r之间存在一组对称关系式:
这两个式子揭示了一元二次方程的根与系数之间的关系,且关系式①②中,x1,x2的地位是对等的(即具有对称性,如将x1,x2互换,原关系式不变).类似地,设一元三次方程x3+px2+qx+r=0(p,q,r为常数)的3个根为x1,x2,x3,则x3+px2+qx+r=(x-x1)(x-x2)(x-x3).由此可得方程x3+px2+qx+r=0的根x1,x2,x3与系数p,q,r之间存在一组对称关系式: , , .
, , . 这两个式子揭示了一元二次方程的根与系数之间的关系,且关系式①②中,x1,x2的地位是对等的(即具有对称性,如将x1,x2互换,原关系式不变).类似地,设一元三次方程x3+px2+qx+r=0(p,q,r为常数)的3个根为x1,x2,x3,则x3+px2+qx+r=(x-x1)(x-x2)(x-x3).由此可得方程x3+px2+qx+r=0的根x1,x2,x3与系数p,q,r之间存在一组对称关系式:
这两个式子揭示了一元二次方程的根与系数之间的关系,且关系式①②中,x1,x2的地位是对等的(即具有对称性,如将x1,x2互换,原关系式不变).类似地,设一元三次方程x3+px2+qx+r=0(p,q,r为常数)的3个根为x1,x2,x3,则x3+px2+qx+r=(x-x1)(x-x2)(x-x3).由此可得方程x3+px2+qx+r=0的根x1,x2,x3与系数p,q,r之间存在一组对称关系式: , , .
, , .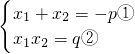 这两个式子揭示了一元二次方程的根与系数之间的关系,且关系式①②中,x1,x2的地位是对等的(即具有对称性,如将x1,x2互换,原关系式不变).类似地,设一元三次方程x3+px2+qx+r=0(p,q,r为常数)的3个根为x1,x2,x3,则x3+px2+qx+r=(x-x1)(x-x2)(x-x3).由此可得方程x3+px2+qx+r=0的根x1,x2,x3与系数p,q,r之间存在一组对称关系式:
这两个式子揭示了一元二次方程的根与系数之间的关系,且关系式①②中,x1,x2的地位是对等的(即具有对称性,如将x1,x2互换,原关系式不变).类似地,设一元三次方程x3+px2+qx+r=0(p,q,r为常数)的3个根为x1,x2,x3,则x3+px2+qx+r=(x-x1)(x-x2)(x-x3).由此可得方程x3+px2+qx+r=0的根x1,x2,x3与系数p,q,r之间存在一组对称关系式: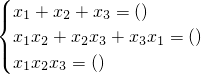 ________,________,________.
________,________,________.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com