有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,

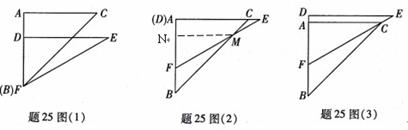
∠FDE=90°,DF=4,DE=.将这副直角三角板按如题25图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.

(1)如题25图(2),当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,

则∠EMC=______度；

(2)如题25图（3），在三角板DEF运动过程中,当EF经过点C时,求FC的长;

(3)在三角板DEF运动过程中,设BF=,两块三角板重叠部分面积为,求与的函数解析式,并求出对应的取值范围.

已知: 关于的方程①.（n≠0）

（1）求证: 方程①必有实数根;

（2）若，为正整数且方程①有两个不相等的整数根时，确定关于的二次函数的解析式；

（3）若把Rt△ABC放在坐标系内，其中∠CAB = 90°，点A、B的坐标分别为（1，0）、（4，0），BC = 5 (点C在第一象限)； 将△ABC沿x轴平移，当点C落在抛物线上时，求△ABC平移的距离.

已知: 关于的方程①.（n≠0）

（1）求证: 方程①必有实数根;

（2）若，为正整数且方程①有两个不相等的整数根时，确定关于的二次函数的解析式；

（3）若把Rt△ABC放在坐标系内，其中∠CAB = 90°，点A、B的坐标分别为（1，0）、（4，0），BC = 5 (点C在第一象限)； 将△ABC沿x轴平移，当点C落在抛物线上时，求△ABC平移的距离.