写出一个有一根为0.且另一根不为0的一元二次方程. .——青夏教育精英家教网—

写出一个有一根为0.且另一根不为0的一元二次方程. . 【查看更多】

如图，抛物线y=ax²+bx+c的顶点为A（4，4），且抛物线经过原点，和x轴相交于另一点B，以AB为一边在直线AB的右侧画正方形ABCD．
（1）求抛物线的解析式和点C、D的坐标；
（2）能否将此抛物线沿着直线x=4平移，使平移后的抛物线恰好经过正方形ABCD的另两个顶点C、D若能，写出平移后抛物线的解析式；若不能，请说明理由；
（3）若以点A（4，4）为圆心，r为半径画圆，请你探究：
①当r=

时，⊙A上有且只有一个点到直线BD的距离等于2；
②当r=

时，⊙A上有且只有三个点到直线BD的距离等于2；
③随着r的变化，⊙A上到直线BD的距离等于2的点的个数也随着变化，请根据⊙

A上到直线BD的距离等于2的点的个数，讨论相应的r的值或取值范围．

查看答案和解析>>

如图，抛物线y=ax²+bx+c的顶点为A（4，4），且抛物线经过原点，和x轴相交于另一点B，以AB为一边在直线AB的右侧画正方形ABCD．
（1）求抛物线的解析式和点C、D的坐标；
（2）能否将此抛物线沿着直线x=4平移，使平移后的抛物线恰好经过正方形ABCD的另两个顶点C、D若能，写出平移后抛物线的解析式；若不能，请说明理由；
（3）若以点A（4，4）为圆心，r为半径画圆，请你探究：
①当r=______时，⊙A上有且只有一个点到直线BD的距离等于2；
②当r=______时，⊙A上有且只有三个点到直线BD的距离等于2；
③随着r的变化，⊙A上到直线BD的距离等于2的点的个数也随着变化，请根据⊙A上到直线BD的距离等于2的点的个数，讨论相应的r的值或取值范围．

查看答案和解析>>

如图，抛物线y＝ax²＋bx＋c的顶点为A(4，4)，且抛物线经过原点，和x轴相交于另一点B，以AB为一边在直线AB的右侧画正方形ABCD．

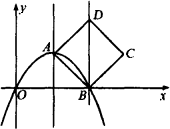
(1)求抛物线的解析式和点C、D的坐标．

(2)能否将此抛物线沿着直线x＝4平移，使平移后的抛物线恰好经过正方形ABCD的另两个顶点C、D？若能，写出平移后抛物线的解析式，若不能，请说明理由．

(3)若以点A(4，4)为圆心，r为半径画圆，请你探究：

①当r＝________时，⊙A上有且只有一个点到直线BD的距离等于2；

②当r＝________时，⊙A上有且只有三个点到直线BD的距离等于2；

③随着的变化，⊙A上到直线BD的距离等于2的点的个数也随着变化，请根据⊙A上到直线BD的距离等于2的点的个数，讨论相应的r的值或取值范围．

查看答案和解析>>

平面直角坐标系中，Rt△ABO的两直角边AO、BO分别在x轴和y轴上，且AO=4，BO=3，Rt△ABO在此坐标系内进行各种运动，但运动停止后始终有一边与原△ABO重合，请你在提供的图18－50上画出运动变化后的三角形的位置(一个坐标系内根据你的需要可画数种变化位置)，并写出另一顶点的坐标．(不必写计算过程)

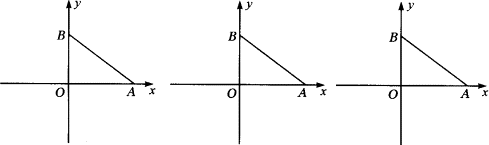
如图答10，分三种情况讨论，(1)以AO为公共边：，，

(2)以BO为公共边：，，

(3)以AB为公共边：，，．

查看答案和解析>>

“相约红色重庆，共享绿色园博”，位于重庆市北部新区的国际园林博览会是一个集自然景观和人文景观为一体的大型城市生态公园．自2011年11月19日开园以来，某商家在园博园内出售纪念品“山娃”玩偶．十周以来，该纪念品深受游人喜爱，其销售量不断增加，销售量y（件）与周数x（1≤x≤10，且x取整数）之间所满足的函数关系如下表所示：

周数x	1	2	3	4	5	6	7	8	9	10
销售量y（件）	110	120	130	140	150	160	170	180	190	200

为回馈顾客，该商家将此纪念品的价格不断下调，其销售单价z（元）与周数x（1≤x≤10，且x取整数）之间成一次函数关系，且第一周的销售单价为68元，第二周的销售单价为66元．另外，已知该纪念品每件的成本为30元．
（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y与x之间的函数关系式；根据题意，直接写出z与x之间满足的一次函数关系式；
（2）求前十周哪一周的销售利润最大，并求出此最大利润；
（3）从十一周开始，其他商家陆续入驻园博园，因此该商店的销售情况不如从前．该纪念品的销售量比十周下降a%（0＜a＜10），于是该商家将此纪念品的销售单价在十周的基础上提高1.4a%．另外，随着园博园管理措施的逐步完善，该商家需每周交纳200元的各种费用．这样，十一周的销售利润恰好与十周持平．请参考以下数据，估算出a的整数值．
（参考数据：22²=484，23²=529，24²=576，25²=625）

查看答案和解析>>

练习册

高中

初中

小学