如图，D．E分别为∆ABC的边AC．BC的中点，则下列说法不正确的是（　　）

A．DE是∆ABC的中线                 B．BD是∆ABC的一条中线

C．CＥ是AB边上的中线      D．BD是边AC上的中线

 

   

 

 

如图，在平面直角坐标系中，∆ABO中，∠AOB=90°,∠ABO=45°,OB=12cm，

O为坐标原点，直线OB为x轴，矩形DEFG的长DE=12cm, 宽EF=6cm，以DE为直径在矩形内作半圆O1，矩形及半圆O1整体以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在x轴上，设运动时间为x（s），矩形和∆ABO的重叠部分的面积为S(cm2).当x=0(s)时，点E与点O重合（如图1）(图（2）、图（3）、图（4）供操作用).

（1）当x=3时，求直线AG的解析式；

（2）当0<x<9时,求S关于x的函数关系式；

（3）当x为何值时，∆ ABC的斜边所在的直线与半圆O1所在的圆相切？

 

 

请尝试解决以下问题：

（1）如图1，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF，求证DE+BF=EF．

感悟解题方法，并完成下列填空：

将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合，

 

 

由旋转可得：AB=AD,BG=DE, ∠1=∠2，∠ABG=∠D=90°,

∴∠ABG+∠ABF=90°+90°=180°，

因此，点G，B，F在同一条直线上．

∵∠EAF=45°  ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°．

∵∠1=∠2，   ∴∠1+∠3=45°．

即∠GAF=∠_________．

又AG=AE，AF=AF

∴△GAF≌_______．

∴_________=EF，故DE+BF=EF．

（2）运用（1）解答中所积累的经验和知识，完成下题：

如图2，在直角梯形ABCD中，AD∥BC（AD＞BC），∠D＝90°，AD＝CD＝10，E是CD上一点，且∠BAE＝45°，DE＝4，求BE的长．

 

 

（2）类比（1）证明思想完成下列问题：在同一平面内，将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，若∆ABC固定不动，∆AFG绕点A旋转，AF、AG与边BC的交点分别为D、E(点D不与点B重合，点E不与点C重合)，在旋转过程中，等式BD+CE=DE始终成立，请说明理由．

 

 

 

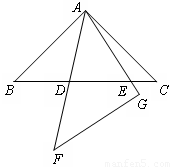
如图，已知∆ABC中，，，D是AB上一动点，DE∥BC，交AC于E，将四边形BDEC沿DE向上翻折，得四边形，与AB、AC分别交于点M、N.

（1）证明：∆ADE ；

（2）设AD为x，梯形MDEN的面积为y，试求y与x的函数关系式. 当x为何值时y有最大值？

 

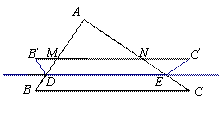如图1，在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，它们的斜边长为2，若∆ABC固定不动，∆AFG绕点A旋转，AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m，CD=n.

（1）请在图中找出两对相似而不全等的三角形，并选取其中一对进行证明.

（2）求m与n的函数关系式，直接写出自变量n的取值范围.

   （3）以∆ABC的斜边BC所在的直线为x轴，BC边上的高所在的直线为y轴，建立平面直角坐标系(如图2).在边BC上找一点D，使BD=CE，求出D点的坐标，并通过计算验证BD＋CE=DE.

   （4）在旋转过程中,(3)中的等量关系BD＋CE=DE是否始终成立,若成立,请证明,若不成立,请说明理由.