
题目列表(包括答案和解析)
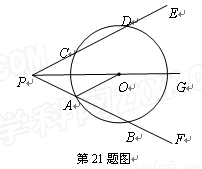
(本题8分)如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF 的两边相交于A、B和C、D,连结OA,此时有OA//PE.
(1)求证:AP=AO;
(2)若tan∠OPB=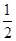 ,求弦AB的长;
,求弦AB的长;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为 ▲ ,能构成等腰梯形的四个点为 ▲ 或 ▲ 或 ▲ .
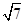 , ∠B=90°.
, ∠B=90°.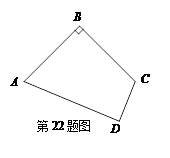
(本题8分) 如图,点O是直线AB上一点,∠AOC=40°,OD平分∠AOC, ∠COE=70°. 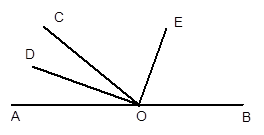
(1)请你说明DO⊥OE;
(2)OE平分∠BOC吗?为什么?
(本题14分)如图,在平面直角坐标系中.四边形OABC是平行四边形.直线 经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒(
经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒( ).△MPQ的面积为S.
).△MPQ的面积为S.
(1)点C的坐标为___________,直线 的解析式为___________.(每空l分,共2分)
的解析式为___________.(每空l分,共2分)
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围。
(3)试求题(2)中当t为何值时,S的值最大,并求出S的最大值。
(4)随着P、Q两点的运动,当点M在线段CB上运动时,设PM的延长线与直线 相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
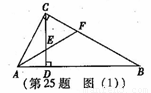
(本题9分)如图(1),Rt△ABC中,∠ACB=-90°,CD⊥AB,垂足为D.AF平分∠CAB,交CD于点E,交CB于点F
(1)求证:CE=CF.
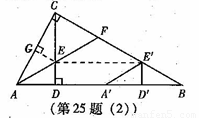
(2)将图(1)中的△ADE沿AB向右平移到△A’D’E’的位置,使点E’落在BC边上,其它条件不变,如图(2)所示.试猜想:BE'与CF有怎样的数量关系?请证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com