阅读下列材料,并回答问题.
画一个直角三角形,使它的两条直角边分别为5和12,那么我们可以量得直角三角形的斜边长为13,并且5
2+12
2=13
2.事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方.如果直角三角形中,两直角边长分别为a、b,斜边长为c,则a
2+b
2=c
2,这个结论就是著名的勾股定理.
请利用这个结论,完成下面的活动:
(1)一个直角三角形的两条直角边分别为6、8,那么这个直角三角形斜边长为
10
10
.
(2)满足勾股定理方程a
2+b
2=c
2的正整数组(a,b,c)叫勾股数组.例如(3,4,5)就是一组勾股数组.观察下列几组勾股数
①3,4,5; ②5,12,13; ③7,24,25;④9,40,41;
请你写出有以上规律的第⑤组勾股数:
11,60,61
11,60,61
.
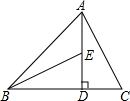
(3)如图,AD⊥BC于D,AD=BD,AC=BE.AC=3,DC=1,求BD的长度.
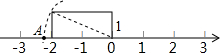
(4)如图,点A在数轴上表示的数是
,请用类似的方法在下图数轴上画出表示数
的B点(保留作图痕迹).


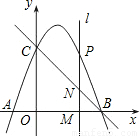
 点,并与x轴交于另一点A.
点,并与x轴交于另一点A.
