
题目列表(包括答案和解析)
.(本题15分)
马田同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),通过计算∠APB的度数,她惊奇的发现∠APB的度数的 ,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
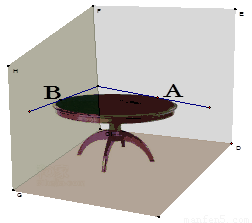 (1)请你求出∠APB的度数
(1)请你求出∠APB的度数
(2)请你求出马田同学作业中的
那条抛物线的对称轴方程.
(本题10分) 随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场。一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售。预计每箱水果的盈利情况如下表:
| | A种水果/箱 | B种水果/箱 |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
(本题8分)2006年3月17日俄罗斯特技飞行队在名胜风景旅游区——张家界天门洞特技表演,其中一架飞机起飞后的高度变化如左下表:
| 高度变化 | 记作 |
| 上升4.5 km |
|
| 下降3.2 km |
|
| 上升1.1 km |
|
| 下降1.4 km |
|
(1)此时这架飞机比起飞点高了多少千米?(2分)
(2)如果飞机每上升或下降1千米需消耗2升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?(3分)
(3)如果飞机做特技表演时,有4个规定动作,起飞后高度变化如下:上升3.8千米,下降2.9千米,再上升1.6千米。若要使飞机最终比起飞点高出1千米,问第4个动作是上升还是下降,上升或下降多少千米?(3分)
(本题10分) 随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场。一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售。预计每箱水果的盈利情况如下表:
|
|
A种水果/箱 |
B种水果/箱 |
|
甲店 |
11元 |
17元 |
|
乙店 |
9元 |
13元 |
有两种配货方案(整箱配货):
方案一:甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱;
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店_________箱,乙店__________箱;B种水果甲店_________箱,乙店__________箱.
(1) 如果按照方案一配货,请你计算出经销商能盈利多少元?
(2) 请你将方案二填写完整(只填写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多?
(3) 在甲、乙两店各配货10箱,且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
(本题6分)如图,在△ABC中,若AB=10,BD=6,AD=8,AC=17,求DC的长。
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com