如图，直线l₁与x轴、y轴分别交于A、B两点，直线l₂与直线l₁关于x轴对称，已知直线l₁的解析式为y=x+3，
（1）求直线l₂的解析式；

（2）过A点在△ABC的外部作一条直线l₃，过点B作BE⊥l₃于E，过点C作CF⊥l₃于F，请画出图形并求证：BE+CF=EF；

（3）△ABC沿y轴向下平移，AB边交x轴于点P，过P点的直线与AC边的延长线相交于点Q，与y轴相交于点M，且BP=CQ，在△ABC平移的过程中，①OM为定值；②MC为定值．在这两个结论中，有且只有一个是正确的，请找出正确的结论，并求出其值．

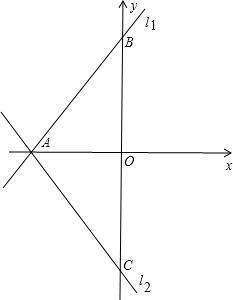
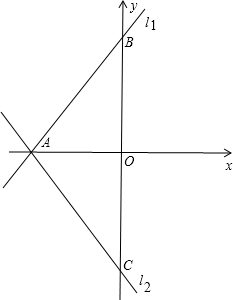
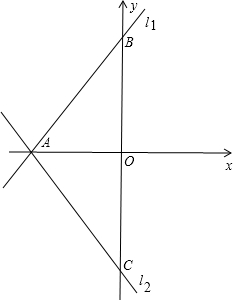
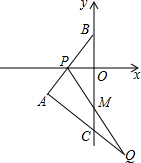
 如图，在平面直角坐标系中，三个机战的坐标分别为，，，延长AC到点D,使CD=,过点D作DE∥AB交BC的延长线于点E.

（1）求D点的坐标；

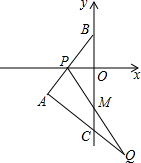
（2）作C点关于直线DE的对称点F,分别连结DF、EF，若过B点的直线将四边形CDFE分成周长相等的两个四边形，确定此直线的解析式；

（3）设G为y轴上一点，点P从直线与y轴的交点出发，先沿y轴到达G点，再沿GA到达A点，若P点在y轴上运动的速度是它在直线GA上运动速度的2倍，试确定G点的位置，使P点按照上述要求到达A点所用的时间最短。（要求：简述确定G点位置的方法，但不要求证明）

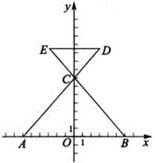
（本小题满分12分）已知：抛物线与x轴交于A、B两点，与y轴交于点C． 其中点A在x轴的负半轴上，点C在y轴的负半轴上，线段OA、OC的长（OA<OC）是方程的两个根，且抛物线的对称轴是直线．

（1）求A、B、C三点的坐标；

（2）求此抛物线的解析式；

（3）若点D是线段AB上的一个动点（与点A、B不重合），过点D作DE∥BC交AC于点E，连结CD，设BD的长为m，△CDE的面积为S，求S与m的函数关系式，并写出自变量m的取值范围．S是否存在最大值？若存在，求出最大值并求此时D点坐标；若不存在，请说明理由．