
题目列表(包括答案和解析)
求证:四边形CEHF为菱形.

图19-2-36
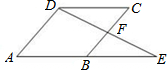 7、如图,已知菱形ABCD,E是AB延长线上一点,连接DE交BC于点F,在不添加任何辅助线的情况下,请补充一个条件,使△CDF≌△BEF,这个条件是
7、如图,已知菱形ABCD,E是AB延长线上一点,连接DE交BC于点F,在不添加任何辅助线的情况下,请补充一个条件,使△CDF≌△BEF,这个条件是 请阅读下列材料:
请阅读下列材料:| PG |
| PC |
| PG |
| PC |
| 3 |
| 3 |
| PG |
| PC |
| 3 |

 (2011•辽阳)如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为
(2011•辽阳)如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为| 3 |
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com