
题目列表(包括答案和解析)
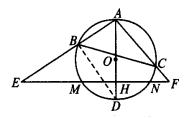
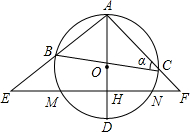
(1)求EH和HF的长;
(2)求BC的长.
 |
| MD |
 |
| DN |
 na=
na=| 3 |
| 4 |
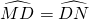 ,EH-HF=2.设∠ACB=a,ta
,EH-HF=2.设∠ACB=a,ta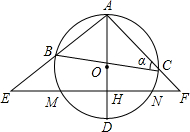 na=
na= ,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.
,EH和HF是方程x2-(k+2)x+4k=0的两个实数根. 如图,AD为⊙O的直径,作⊙O的内接等边三角形ABC.黄皓、李明两位同学的作法分别是:
如图,AD为⊙O的直径,作⊙O的内接等边三角形ABC.黄皓、李明两位同学的作法分别是:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com