题目列表(包括答案和解析)
2011年3月16日上午10时福岛第一核电站第3号反应堆发生了爆炸。为了抑制核辐射进一步扩散，日本决定向6号反应堆注水冷却，铀棒被放在底面积为100m2、高为20m的长方体水槽中的一个圆柱体桶内，如图（1）所示，向桶内注入流量一定的水，注满后，继续注水，直至注满水槽为止（假设圆柱体桶在水槽中的位置始终不改变）。水槽中水面上升的高度h与注水时间t之间的函数关系如图（2）所示。
(1)求圆柱体的底面积；(2)若的圆柱体高为9m，求注水的速度及注满水槽所用时间。
h(cm)
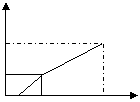
O 18 90 20 t(s)
|
已知：如图（1），点G是BC的中点，点H在AF上，动点P以每秒
的速度沿图（1）的边线运动，运动路径为：相应的
的面积
关于运动时间
的函数图象如图（2），若
则下列四个结论中正确的个数有（ ）
A、 图（1）中的BC边长是8
B、 图（2）中的M点表示第4秒时
的值为24
C、 图（1）中的CD长是4，
D、 图（2）中的N点表示第12秒时的值为18
| （1） | |
 |
（2）
A、 1个 B、2个 C、 3个 D、 4个
行驶中的汽车，在刹车后由于惯性的作用，还要继续向前滑行一段距离才能停止，这段距离称为“刹车距离”．为了测定某型号汽车的刹车性能(车速度不能超过140km/h)，对这种汽车进行测试，测得数据如下：
|
刹车时车速（km/h） |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
|
刹车距离（m） |
0 |
0.3 |
1.0 |
2.1 |
3.6 |
5.5 |
7.8 |
(1)以车速为x轴，以刹车距离为y轴，在坐标系中描出这些数据所表示的点，并用平滑的曲线连结这些点，得到函数的大致图像；
(2)观察图像，估计函数的类型．
(3)如果该函数解析式为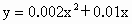
，若该型号汽车在国道上发生了一次交通事故，现场测得刹车距离为46.5m，请推测刹车时的速度．在事故发生时，汽车是超速行驶还是正常行驶？
服 务 项 目 计划A 计划B
即时直接对话＋自动数字传呼 即时直接对话＋自动数字传呼
每月基本服务费（座机费） 50元 98元
免费通话时间 首60分钟 首300分钟
以后每分钟收费 0.40元 0.40元
请根据上面提供的信息，解答下列问题：
（1）设通话时间为
（分钟），所需付出的费用为
（元）。分别写出计划A、计划B中的
与
之间的函数关系式；
（2）通话时间超过多少分钟时，计划B才会比计划A更优？
（3）若用户决定选择计划B，最多可以比选择A便宜多少费用？
反比例函数y＝
(k≠0)任取一点M(a，b)，过M作MA⊥x轴，MB⊥y轴，所得矩形OAMB的面积为S＝MA·MB＝|b|·|a|＝|ab|．又因为b＝
，故ab＝k，所以S＝|k|(如图(1))．
这就是说，过双曲线上任意一点作x轴、y轴的垂线，所得的矩形面积为|k|．这就是k的几何意义，会给解题带来方便．现举例如下：
例1：如(2)图，已知点P1(x1，y1)和P2(x2，y2)都在反比例函数y＝
(k＜0)的图像上，试比较矩形P1AOB与矩形P2COD的面积大小．
解答：
＝|k|
＝|k|
故＝
例2：如图(3)，在y＝
(x＞0)的图像上有三点A、B、C，经过三点分别向x轴引垂线，交x轴于A1、B1、C1三点，连结OA、OB、OC，记△OAA1、△OBB1、△OCC1的面积分别为S1、S2、S3，则有( )
A．S1＝S2＝S3
B．S1＜S2＜S3
C．S3＜S1＜S2
D．S1＞S2＞S3
解答：∵
＝
|k|＝，
＝|k|＝
＝|k|＝
S1＝S2＝S3，故选A．
例3：一个反比例函数在第三象限的图像如图(4)所示，若A是图像任意一点，AM⊥x轴，垂足为M，O是原点，如果△AOM的面积是3，那么这个反比例函数的解析式是________．
解答：∵S△AOM＝
|k|
又S△AOM＝3，
∴|k|＝3，|k|＝6
∴k＝±6
又∵曲线在第三象限
∴k＞0∴k＝6
∴所以反比例函数的解析式为y＝
．
根据是述意义，请你解答下题：
如图(5)，过反比例函数y＝
(x＞0)的图像上任意两点A、B分别作轴和垂线，垂足分别为C、D，连结OA、OB，设AC与OB的交点为E，△AOE与梯形ECDB的面积分别为S1、S2，比较它们的大小，可得
A．S1＞S2
B．S1＝S2
C．S1＜S2
D．大小关系不能确定
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com