（本小题满分10分）如图，小丽的家住在世通华庭的电梯公寓AD内，她家的对面新建了一座大厦BC。为了测得大厦的高度，小丽在她家的楼底A处测得大厦顶部B的仰角为60º，爬上楼顶D处测得大厦的顶部B的仰角为30º。已知小丽所住的电梯公寓高82米，请你帮助小丽计算出大厦高度BC及大厦与小丽所住电梯公寓间的距离AC。
（计算结果保留根号）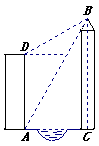

（本小题满分10分）

某商场将进价40元一个的某种商品按50元一个售出时，每月能卖出500个.商场想了两个方案来增加利润：

方案一：提高价格，但这种商品每个售价涨价1元，销售量就减少10个；

方案二：售价不变，但发资料做广告。已知这种商品每月的广告费用m(千元)与销售量倍数p关系为p =  ；

试通过计算，请你判断商场为赚得更大的利润应选择哪种方案？请说明你判断的理由！

（本小题满分10分）

某工厂计划为震区生产两种型号的学生桌椅500套，以解决1250名学生的学习问题，一套型桌椅（一桌两椅）需木料，一套型桌椅（一桌三椅）需木料，工厂现有库存木料．

1.（1）有多少种生产方案？

2.（2）现要把生产的全部桌椅运往震区，已知每套型桌椅的生产成本为100元，运费2元；每套型桌椅的生产成本为120元，运费4元，求总费用（元）与生产型桌椅（套）之间的关系式，并确定总费用最少的方案和最少的总费用．（总费用生产成本运费）

3.（3）按（2）的方案计算，有没有剩余木料？如果有，请直接写出用剩余木料再生产以上两种型号的桌椅，最多还可以为多少名学生提供桌椅；如果没有，请说明理由．

（2011广西崇左，22，10分）（本小题满分10分）矩形、菱形、正方形都是平行四边形，但它们都是有特殊条件的平行四边形，正方形不仅是特殊的矩形，也是特殊的菱形.因此，我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题：
（1）将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.

（2）要证明一个四边形是正方形，可先证明四边形是矩形，再证明这个矩形的_______相等；或者先证明四边形是菱形，在证明这个菱形有一个角是________ .
（3）某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a²，对此结论，你认为是否正确？若正确，请说明理由；若不正确，请举出一个反例说明.