练习册

  • 练习册
  • 试题
    三角形全等的判定方法:⑴一般三角形全等的判定方法:①SSS,②SAS,③ASA,④AAS. ⑵直角三角形全等的判定方法:①SSS,②SAS,③ASA,④AAS,⑤HL. 【查看更多】

     

    题目列表(包括答案和解析)

    全等三角形的判定方法：对于一般三角形我们可以用“________”、“________”、“________”、“________”这四种方法来判定全等．而对于直角三角形，我们除了可以运用上述四种方法判定全等外，还可以利用一种特殊的判定方法，即“________”．由此，要判定两个三角形全等，至少要有一组________对应相等．

    查看答案和解析>>

    阅读下面的题目及分析过程，并按要求进行证明．

    已知：如图，是的中点，点在上，且．

        求证：.

        分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等．因此，要证，必须添加适当的辅助线，构造全等三角形或等腰三角形．

       现给出如下三种添加辅助线的方法，请任意选择其中一种，对原题进行证明．

     


    查看答案和解析>>

    全等三角形的性质与判定

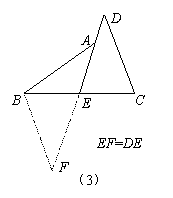    (1)性质：全等三角形的__________相等，__________相等，对应角的平分线、对应边上的中线和高对应相等．

    通过三角形全等证明线段相等、角相等是一种重要方法，是本章的一个重点．

    (2)判定：一般三角形全等的判定方法有__________，直角三角形全等的判定方法除上述方法外还有__________(填简写符号)．

     

    查看答案和解析>>

    阅读下面的题目及分析过程，并按要求进行证明。
    已知：如图，E是BC的中点，点A在DE上，且∠BAE=∠CDE
    求证：AB=CD
    分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等。因此，要证明AB=CD，必须添加适当的辅助线，构造全等三角形或等腰三角形。现给出如下三种添加辅助线的方法，请对原题进行证明。
    （1）延长DE到F使得EF=DE；
    （2） 作CG⊥DE于G，BF⊥DE于F交DE的延长线于F ；
    （3） 过C点作CF∥AB，交DE的延长线于F 

    查看答案和解析>>

    阅读下面的题目及分析过程，并按要求进行证明．
    已知：如图，E是BC的中点，点A在DE上，且∠BAE=∠CDE，求证：AB=CD．
    分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等．因此，要证明AB=CD，必须添加适当的辅助线，构造全等三角形或等腰三角形．
    现给出如下三种添加辅助线的方法，请任意选择其中两种对原题进行证明．

    图（1）：延长DE到F使得EF=DE
    图（2）：作CG⊥DE于G，BF⊥DE于F交DE的延长线于F
    图（3）：过C点作CF∥AB交DE的延长线于F．

    查看答案和解析>>


    同步练习册答案