
题目列表(包括答案和解析)
某商业公司为指导某种应季商品的生产和销售,对三月份至七月份该商品的售价和成本进行了调研,结果如下:每件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图1),每件商品的成本Q(元)与时间t(月)的关系可用一条抛物线的一部分上的点来表示(如图2)。
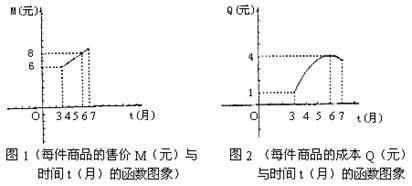
(说明:图1、图2中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本。)
请你根据图象提供的信息回答:
(1)每件商品在3月份出售时的利润(利润=售价-成本)是多少元?
(2)求图2中表示的每件商品的成本Q(元)与时间t(月)之间的函数关系式(不要求写自变量的取值范围);
(3)你能求出三月份至七月份每件商品的利润W(元)与时间t(月)之间的函数关系式吗?(请写出计算过程,不要求写自变量的取值范围)若该公司共有此种商品30000件,准备在一个月内全部售完,请你计算一下至少可获利多少元?
某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求该机器的生产数量;
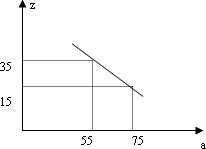
(3)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价-成本)
已知二次函数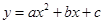 中,其函数
中,其函数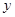 与自变量
与自变量 之间的部分对应值如下表所示:
之间的部分对应值如下表所示:
| x | …… | 0 | 1 | 2 | 3 | 4 | 5 | …… |
| y | …… | 4 | 1 | 0 | 1 | 4 | 9 | …… |
 ,
,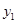 )、B(
)、B(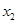 ,
,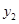 )在该函数的图象上,则当
)在该函数的图象上,则当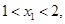
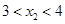 时,
时,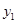 与
与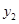 的大小关系是 ;
的大小关系是 ;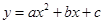 的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?=】
的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?=】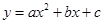 中,其函数
中,其函数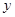 与自变量
与自变量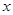 之间的部分对应值如下表所示:
之间的部分对应值如下表所示:| x | …… | 0 | 1 | 2 | 3 | 4 | 5 | …… |
| y | …… | 4 | 1 | 0 | 1 | 4 | 9 | …… |
 ,
,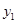 )、B(
)、B(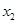 ,
,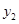 )在该函数的图象上,则当
)在该函数的图象上,则当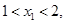
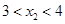 时,
时,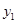 与
与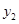 的大小关系是 ;
的大小关系是 ;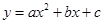 的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?=】
的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?=】平面直角坐标中,对称轴平行于y轴的抛物线经过原点O,其顶点坐标为(3,-![]() );Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(
);Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(![]() ,0),且BC=5,AC=3(如图(1)).
,0),且BC=5,AC=3(如图(1)).
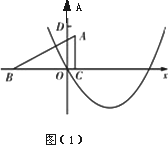
(1)求出该抛物线的解析式;
(2)将Rt△ABC沿x轴向右平移,当点A落在(1)中所求抛物线上时Rt△ABC停止移动.D(0,4)为y轴上一点,设点B的横坐标为m,△DAB的面积为s.
①分别求出点B位于原点左侧、右侧(含原点O)时,s与m之间的函数关系式,并写出相应自变量m的取值范围(可在图(1)、图(2)中画出探求);

②当点B位于原点左侧时,是否存在实数m,使得△DAB为直角三角形?若存在,直接写出m的值;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com