
题目列表(包括答案和解析)
(本题10分)如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上
(Ⅰ)求AB边上的高CE所在直线的方程
(Ⅱ)求△ABC的面积
(本题10分)如图一边长为48cm的正方形铁皮,四角各截去一个大小相同的小正方形,然后折起,可以做成一个无盖长方体容器。所得容器的体积V(单位: )是关于截去的小正方形的边长x(单位:
)是关于截去的小正方形的边长x(单位: )的函数。⑴ 随着x的变化,容积V是如何变化的?
)的函数。⑴ 随着x的变化,容积V是如何变化的?
⑵ 截去的小正方形的边长为多少时,容器的容积最大?最大容积是多少?












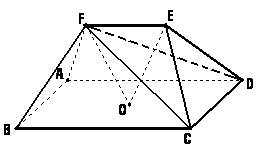 (本题10分) 如图,在五面体EF-ABCD中,点O是矩形ABCD的对角线的交点,△CDE是等边三角形,棱
(本题10分) 如图,在五面体EF-ABCD中,点O是矩形ABCD的对角线的交点,△CDE是等边三角形,棱 ![]()
(1)证明FO//平面CDE;
(2)设![]() ,证明EO⊥平面CDF.
,证明EO⊥平面CDF.
(本题满分10分) 如图, 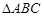 内接于⊙
内接于⊙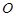 ,
, 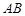 是⊙
是⊙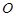 的直径,
的直径, 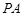 是过点
是过点 的直线, 且
的直线, 且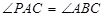 .
.

(Ⅰ) 求证: 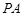 是⊙
是⊙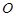 的切线;
的切线;
(Ⅱ)如果弦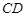 交
交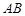 于点
于点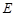 ,
, 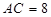 ,
,
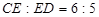 ,
, 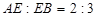 , 求
, 求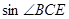 .
.
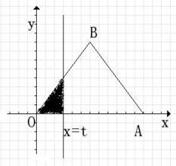
(本题满分10分)如图,△OAB是边长为2的正三角形,记△OAB位于直线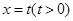 左侧的图形的面积为
左侧的图形的面积为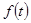 。试求函数
。试求函数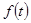 的解析式,并画出函数
的解析式,并画出函数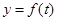 的图象.
的图象.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com