
题目列表(包括答案和解析)
(本小题满分14分)如图,已知三角形PAQ顶点P(-3,0),点A在y轴上,点Q在x轴正半轴上,![]() ·
·![]() =0,
=0, ![]() =2
=2![]() .(1)当点A在y轴上移动时,求动点M的轨迹E的方程;
.(1)当点A在y轴上移动时,求动点M的轨迹E的方程;
(2)设直线l:y=k(x+1)与轨迹E交于B、C两点,点D(1,0),若∠BDC为钝角,求k的取值范围.
(本小题满分14分)如图所示,某市政府决定在以政府大楼O为中心、正北方向
和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考
虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正
面要朝市政府大楼.设扇形的半径OM=R ,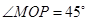 ,OB与OM之间的夹角为
,OB与OM之间的夹角为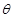 .
.
(1)将图书馆底面矩形ABCD的面积S表示成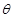 的函数.
的函数.
(2)若 R=45 m,求当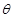 为何值时,矩形ABCD的面积S有最大值?
为何值时,矩形ABCD的面积S有最大值?
其最大值是多少?
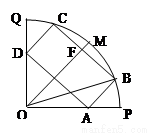
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com