练习册

  • 练习册
  • 试题
    1．cos75 o·cos15o= , 【查看更多】

     

    题目列表(包括答案和解析)

    （2012•杭州二模）如图所示，A，B，C是圆O上的三点，CO的延长线与线段BA的延长线交于圆O外的点D，若
    OC
    =m
    OA
    +n
    OB
    ，则m+n的取值范围是（　　）

    查看答案和解析>>

    已知O是△ABC内任意一点，连接AO、BO、CO并延长交对边于A′、B′、C′，则
    OA′
    AA′
    +
    OB′
    BB′
    +
    OC′
    CC′
    =1    ，运用类比猜想，对于空间中四面体A-BCD有
    OA′
    AA′
    +
    OB′
    BB′
    +
    OC′
    CC′
    +
    OD′
    DD′
    =1
    OA′
    AA′
    +
    OB′
    BB′
    +
    OC′
    CC′
    +
    OD′
    DD′
    =1
    ．

    查看答案和解析>>

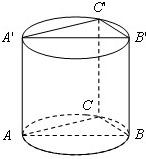    精英家教网如图，直三棱柱ABC-A′B′C′内接于高为
    		2
    的圆柱中，已知∠ACB=90°，AA′=
    		2
    ，BC=AC=1，O为AB的中点．
    求（1）圆柱的全面积；
    （2）异面直线AB′与CO所成的角的大小；
    （3）求二面角A′-BC-A的大小．

    查看答案和解析>>

    对于平面内的命题：“△ABC内接于圆O，圆O的半径为R，且O点在△ABC内，连接AO，BO，CO并延长分别交对边于A1，B1，C1，则AA1+BB1+CC1≥
    9R
    2
    ”．
    证明如下：
    OA1
    AA1
    +
    OB1
    BB1
    +
    OC1
    CC1
    =
    S△OBC
    S△ABC
    +
    S△OAC
    S△ABC
    +
    S△OAB
    S△ABC
    =1    ，
    即：
    AA1-R
    AA1
    +
    BB1-R
    BB1
    +
    CC1-R
    CC1
    =1    ，即
    1
    AA1
    +
    1
    BB1
    +
    1
    CC1
    =
    2
    R
    ，
    由柯西不等式，得(AA1+BB1+CC1)(
    1
    AA1
    +
    1
    BB1
    +
    1
    CC1
    )≥9    ．∴AA1+BB1+CC1≥
    9R
    2
    ．
    将平面问题推广到空间，就得到命题“四面体ABCD内接于半径为R的球O内，球心O在该四面体内，连接AO，BO，CO，DO并延长分别与对面交于A1，B1，C1，D1，则
    AA1+BB1+CC1+DD1≥
    16R
    3
    AA1+BB1+CC1+DD1≥
    16R
    3
    ”．

    查看答案和解析>>

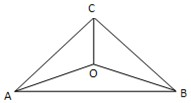    如图，某地有两家工厂，分别位于等腰直角△ABC的两个顶点A、B处，AB=20km．为了处理这两家工厂的污水，现要在该三角形区域（含边界）内且与A、B等距的一点O处，建造一个污水处理厂，并铺设排污管道AO、BO．记铺设管道的总长度为ykm．
    （1）设AO=xkm，将y表示成关于x的函数；
    （2）设CO=tkm，将y表示成关于t的函数．

    查看答案和解析>>


    同步练习册答案