
题目列表(包括答案和解析)
(08年泉州一中适应性练习文)甲、乙、丙三位同学上课后独立完成5道自我检测题,甲及格概率为![]() ,乙及格概率为
,乙及格概率为![]() ,丙及格概率为
,丙及格概率为![]() ,则三人中至少有一人及格的概率为( )
,则三人中至少有一人及格的概率为( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
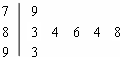 某年级举行校园歌曲演唱比赛,七位评委为学生甲打出的演唱分数茎叶图如图所示,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为
某年级举行校园歌曲演唱比赛,七位评委为学生甲打出的演唱分数茎叶图如图所示,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为A、
| ||
B、
| ||
C、
| ||
D、
|
 在某项体育比赛中,七位裁判为一选手打出分数的茎叶图如图,去掉一个最高分和一个摄低分后,该选手的平均分为( )
在某项体育比赛中,七位裁判为一选手打出分数的茎叶图如图,去掉一个最高分和一个摄低分后,该选手的平均分为( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com