
题目列表(包括答案和解析)
有以下几个命题
①若函数 是连续函数,则
是连续函数,则![]() 的值是±1;
的值是±1;
②由一组样本数据(x1,y1),(x2,y2),…,(xn,yn)得到的回归直线方程为![]() ,直线
,直线![]() 必经过点
必经过点![]() ;
;
③设A、B为两个定点,m(m>0)为常数,![]() ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;
④若数列{an}是递增数列,且an=n2+λn+1(n≥2,n∈N*),则实数λ的取值范围
是(-5,+∞);
⑤若椭圆的左、右焦点分别为F1、F2,P是该椭圆上的任意一点,则点F2关于∠F1PF2的外角平分线对称的点M的轨迹是圆.
其中真命题的序号为________;(写出所有真命题的序号)
有以下几个命题
①一个容量为n的样本,分成若干组,已知某组的频数和频率分别为40和0.125,则n的值为320;
②设A、B为两个定点,m(m>0)为常数,![]() ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;
③若数列{an}是递增数列,且an=n2+λn+1(n≥2,n∈N*),则实数λ的取值范围是(-5,+∞);
④若椭圆的左、右焦点分别为F1、F2,P是该椭圆上的任意一点,则点F2关于∠F1PF2的外角平分线对称的点M的轨迹是圆.
其中真命题的序号为________;(写出所有真命题的序号)
 ,f(-
,f(- ))对称:
))对称: x3-
x3- x2-
x2- ,则,g(
,则,g( )+g(
)+g( )+g(
)+g( )+…+g(
)+…+g( )=-105.5.
)=-105.5.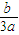 ,f(-
,f(-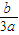 ))对称:
))对称: x3-
x3- x2-
x2-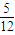 ,则,g(
,则,g(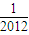 )+g(
)+g(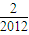 )+g(
)+g(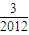 )+…+g(
)+…+g(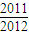 )=-105.5.
)=-105.5. ,f(-
,f(- ))对称:
))对称: x3-
x3- x2-
x2- ,则,g(
,则,g( )+g(
)+g( )+g(
)+g(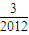 )+…+g(
)+…+g( )=-105.5.
)=-105.5.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com