（本小题满分16分）
如图，实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成，圆P和圆Q的半径都是2km，点P在圆Q上，现要在公园内建一块顶点都在圆P上的多边形活动场地．
（1）如图甲，要建的活动场地为△RST，求场地的最大面积；
（2）如图乙，要建的活动场地为等腰梯形ABCD，求场地的最大面积．

（本小题满分16分）

如图，实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成，圆P和圆Q的

半径都是2km，点P在圆Q上，现要在公园内建一块顶点都在圆P上的多边形活动场地．

（1）如图甲，要建的活动场地为△RST，求场地的最大面积；

（2）如图乙，要建的活动场地为等腰梯形ABCD，求场地的最大面积．

（本小题满分16分）如图，某市拟在长为8km的道路的一侧修建一条运动赛道，赛道的前一部分为曲线段该曲线段为函数的图象，且图象的最高点为；赛道的后一部分为折线段，为保证参赛运动员的安全，限定．

（1）求，的值和，两点间的距离；

（2）设，请把折线段赛道的长度表示成的函数（需写出定义域），当取何值时，最长，最长值是多少？

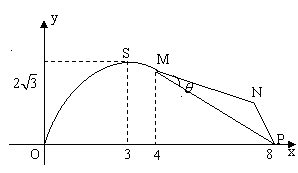
（本小题满分16分）如图，某市拟在长为8km的道路的一侧修建一条运动赛道，赛道的前一部分为曲线段该曲线段为函数的图象，且图象的最高点为；赛道的后一部分为折线段，为保证参赛运动员的安全，限定．

（1）求，的值和，两点间的距离；

（2）设，请把折线段赛道的长度表示成的函数（需写出定义域），当取何值时，最长，最长值是多少？

（本小题满分16分）

某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其在

40分钟的一节课中，注意力指数p与听课时间t（单位：分钟）之间的关系满足如图

所示的曲线．当时，曲线是二次函数图象的一部分，当时，曲线

是函数(，)图象的一部分．根据专家研究，当注意力指数p大于80时学习效果最佳．

（1）试求的函数关系式；

（2）教师在什么时段内安排核心内容，能使得学生学习效果最佳？请说明理由．