
题目列表(包括答案和解析)
请同学们动手做一做这个实验:将塑料瓶底部扎一小孔做成一漏斗,再挂在架子上,就做成了一个简易的单摆.在漏斗下方放一块纸板,板中间画一条直线作为坐标系的横轴.把漏斗灌上细沙并拉离平衡位置,放手使它摆动.同时匀速拉动纸板,这样可在纸板上得到一条曲线,如图,它表示了漏斗对平衡位置的位移s(纵坐标)随时间t(横坐标)变化情况.
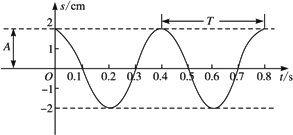
请思考下面问题:
1.根据上节内容,请从图象判定它是否为周期函数?若是,周期是多少?
2.仔细想一想,依据图象的特征,你还能从图象中得到什么启示?
| 2n |
 |
| i=1 |
| 2n |
 |
| i=1 |
| 1 | ||
|
| AB |
| a2+λb2 |
| 1+λ |
| a+λb |
| 1+λ |
| log2010a+log2010b |
| 1+λ |
| a+λb |
| 1+λ |
| log2010a+log2010b |
| 1+λ |
| a+λb |
| 1+λ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com