
题目列表(包括答案和解析)
(本小题14分)如图,吊车的车身高为m米(包括车轮的高度),吊臂长n米,现要把一个直径为6米,高为3米的圆柱形屋顶水平地吊到屋基上安装,在安装过程中屋顶不能倾斜(注:在吊臂的旋转过程中可以靠吊起屋顶的缆绳的伸缩使得屋顶保持水平状态).
(I)设吊臂与水平面的倾斜角为![]() ,屋顶底部与地面间的距离最大为
,屋顶底部与地面间的距离最大为![]() 米,此时如图所示,屋顶上部与吊臂有公共点,试将h表示为
米,此时如图所示,屋顶上部与吊臂有公共点,试将h表示为![]() 函数,并写出定义域;
函数,并写出定义域;
(II)若某吊车的车身高为![]() 米,吊臂长24米,使用该吊车将屋顶吊到14米的屋基上,能否吊装成功?
米,吊臂长24米,使用该吊车将屋顶吊到14米的屋基上,能否吊装成功?

(本小题满分14分)(注意:在试题卷上作答无效)
设数列 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 都在函数
都在函数 的图象上.
的图象上.
(Ⅰ)求 及数列
及数列 的通项公式
的通项公式 ;
;
(Ⅱ) 将数列 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),( ,
, ,
, ,
, );(
);( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),( ,
, ,
, ,
, );(
);( ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为 ,求
,求 的值;
的值;
(Ⅲ)令 (
( ),求证:
),求证:
(本小题满分14分)(注意:在试题卷上作答无效)
设数列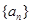 的前
的前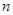 项和为
项和为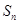 ,对一切
,对一切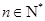 ,点
,点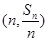 都在函数
都在函数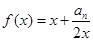 的图象上.
的图象上.
(Ⅰ)求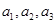 及数列
及数列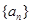 的通项公式
的通项公式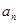 ;
;
(Ⅱ) 将数列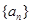 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为(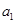 ),(
),( ,
,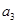 ),(
),(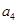 ,
,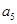 ,
,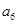 ),(
),(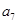 ,
,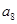 ,
,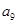 ,
, );(
);(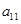 ),(
),(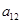 ,
,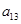 ),(
),(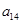 ,
,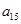 ,
,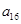 ),(
),(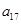 ,
,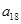 ,
,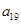 ,
,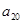 );(
);(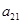 ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为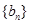 ,求
,求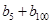 的值;
的值;
(Ⅲ)令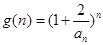 (
( ),求证:
),求证: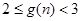
(本小题共14分)
已知函数
(1)试用含有a的式子表示b,并求 的单调区间;
的单调区间;
(2)设函数 的最大值为
的最大值为 ,试证明不等式:
,试证明不等式:
(3)首先阅读材料:对于函数图像上的任意两点 ,如果在函数图象上存在点
,如果在函数图象上存在点 ,使得
,使得 在点M处的切线
在点M处的切线 ,则称AB存在“相依切线”特别地,当
,则称AB存在“相依切线”特别地,当 时,则称AB存在“中值相依切线”。
时,则称AB存在“中值相依切线”。
请问在函数 的图象上是否存在两点
的图象上是否存在两点 ,使得AB存在“中值相依切线”?若存在,求出一组A、B的坐标;若不存在,说明理由。
,使得AB存在“中值相依切线”?若存在,求出一组A、B的坐标;若不存在,说明理由。
(本小题满分14分)
设关于 的函数
的函数 ,其中
,其中 为
为 上的常数,若函数
上的常数,若函数 在
在 处取得极大值
处取得极大值 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若函数 的图象与直线
的图象与直线 有两个交点,求实数
有两个交点,求实数 的取值范围;
的取值范围;
(Ⅲ)设函数 ,若对任意地
,若对任意地 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com