
题目列表(包括答案和解析)
一刀切豆腐将豆腐切为2块,两刀切豆腐最多可将豆腐切为4块,问三刀切豆腐最多可将豆腐切为几块,怎么切?试作出图形.
[分析] 本题实际上是三个平面将空间最多分成几部分的问题,画这种平面分割空间的直观图,其实就是考查相交平面的画法,画图时要注意画相交平面的顺序和虚、实线的选择.
| v1+v2 |
| 2 |
1.B解析:本题考察函数零点概念,要注意函数零点是函数对应方程的根,是一数而不是点
从标有1~10的10支竹签中任取2支,设所得2支竹签上的数字之和为X,那么随机变量X可能的取值有( )
A.17个 B.18个 C.19个 D.20个
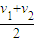 (甲、乙两人中途不停歇),则甲、乙两人上下山所用的时间t1,t2的关系为( )
(甲、乙两人中途不停歇),则甲、乙两人上下山所用的时间t1,t2的关系为( )(1)数列中有多少项是负数?
(2)n为何值时,an与n之间构成二次函数关系,可结合二次函数知识去进行探求,同时要注意n的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com