
题目列表(包括答案和解析)
为了让学生更多的了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有 名学生参加了这次竞赛.为解本 次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为
名学生参加了这次竞赛.为解本 次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为 分)进行统计.请你根据频率分布表,解答下列问题:
分)进行统计.请你根据频率分布表,解答下列问题:
(Ⅰ)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
|
序号( |
分组(分数) |
组中值 |
频数(人数) |
频率 |
|
|
|
|
① |
|
|
|
|
|
|
② |
|
|
|
|
③ |
|
|
|
|
|
④ |
⑤ |
|
合计 |
|
|
(Ⅱ)为鼓励更多的学生了解“数学史”知识,成绩不低于 分的同学能获奖,请估计在参加的
分的同学能获奖,请估计在参加的 名学生中大概有多少同学获奖?
名学生中大概有多少同学获奖?
(Ⅲ)在上述统计数据的分析中有一项计算
|
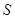 的值.
的值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com